Human-Aligned Large Language Models
About recent LLM alignment finetuning techniques such as RLHF, DPO, KTO, IPO and SPIN
Table of Content
A Bit of Context
In alignment training, the goal is to ensure that the outputs generated by machine learning models align closely with human preferences, values, and intentions. The research traces back to the classic era of machine learning, studying preference models to support various tasks in classification and reinforcement learning [1,2]. Until 2017, researchers have scaled up the approach and employed reinforcement learning algorithms such as PPO in aligning models to predict according to human preference [3]. As Large Language Models become more prevalent, alignment training emerges as a crucial factor in their success, especially in the case of Chat-GPT. The LLM finetuning framework generally consists of two steps:
Supervised finetuning: LLM is finetuned on data with ground truth labels for the task.
Alignment finetuning: LLM is finetuned on human feedback data, often in the form of preference such as comparison feedback.
🧠 Why is alignment necessary instead of keeping supervised fine-tuning?
Limited training data leads to overfitting with excessive fine-tuning.
Obtaining more supervised data requires costly labeling of ground truth answers.
Supervised fine-tuning using LLM is expensive and does not prioritize generating user-desired outputs.
👉 This article focuses on step 2: LLM alignment. A common scheme for alignment training is to use feedback-based labels as training signals to reduce the labeling cost. Another consideration is that the finetuned model should not deviate too much from the base model, ensuring that the final model retains the properties learned from extensive pretraining and supervised tuning data.
Reinforced Finetuning using Reward Model
Originated from the situation where human feedback is employed to optimize RL policy, the approach, named Reinforcement learning with human feedback (RLHF, [3]), involves 2 phases: (1) reward learning and (2) policy optimization, as depicted in the schematic diagram below:

Put in the context of LLM in practice, we need to collect dataset D of training data from humans. Here, the Reinforcement Learning (RL) agent is represented by the LLM itself, operating within a one-step episode environment. In this setup, the LLM executes a single action to generate complete output responses [4].
Reward Learning
Collecting preference data is one of the most efficient ways to get data from humans. In particular, preference data is generated by sampling two response outputs from a policy (normally a pretrained LLM) and presenting them to an agent (normally a human) for rating to indicate which one is preferred.
To model human preference, the authors in [3,4] choose the Bradley-Terry model:
where p*(y1≻y2|x) denotes the true (human) probability y1 is preferred to y2 given input x. Here, r* is the true reward function assigning a scalar score to indicate the output y's suitability to input x. In practice, we can only estimate the true reward by training a reward model rθ to minimize the negative log-likelihood of p*(y1≻y2|x) according to the preference data D as follows,
where yw and yl are the preferred and dispreferred response, respective. With σ as the sigmoid function, the loss is simply the negative expected log-likelihood of the Bradley-Terry preference distribution. Here, (K, 2) is the number of response pairs from generated K responses, all presented to humans for rating. The reward learning process is summarized below:

Policy Optimization
Given the reward, any policy gradient method can be used to update the LLM’s parameters to maximize the expected reward. The authors in [4] selected PPO as the optimization algorithm. They augmented it with regularization terms to restrict updates from deviating too significantly from the base model, a supervised fine-tune model (SFT). The regularization involves applying per-token KL divergence penalties from the base model to each token, aiming to mitigate over-optimization of the reward model. In addition, the authors also explore the integration of pretraining gradients into PPO gradients by introducing another regularization loss, which is the log-likelihood of the optimized policy on pertaining data. The final RL objective is:
Although this training scheme is the cornerstone for the success of Chat-GPT, it faces several limitations:
❌ It may face instability and require significant computational resources.
❌ It involves 2 cumbersome phases: reward model training and reinforcement learning fine-tuning.
👉 Coordinating these phases can be challenging due to varied hyperparameters and human feedback dynamics
AI Feedback
Gathering high-quality human preference labels for RLHF is time-consuming and expensive. RLAIF [9,10] offers a promising alternative, using a powerful LLM to generate preferences instead. The picture below summaries the two pipelines:

The off-the-shelf LLM is a general-use but not specifically fine-tuned model for a downstream task. There are two approaches to prompt the off-the-shelf LLM:
The LLM is tasked with rating which response is preferred when presented with a piece of text and two candidate responses.
The LLM is directly prompted for reward scores during RL, bypassing the step of distilling LLM preference labels into a reward model.
👀 There are several tricks to ensure the quality of generated preference labels. For example, to reduce position bias in preference labeling, the authors in [10] conduct two inferences for each pair of candidates. In the second inference, the order of candidate presentation to the LLM is reversed. The results from both inferences are averaged to obtain the final preference distribution.
Preference Optimization without RL
A recent breakthrough [5] in LLM alignment reveals the possibility of directly optimizing the LLM to align with preference data, eliminating the necessity for reward learning 👉 DPO. This paradigm shift is illustrated below:
Direct Preference Optimization (DPO)
The key idea is that for a given reward function r, the main RLHF optimization objective with reward and KL divergence terms have a closed-form solution of the optimal policy:
The problem with this closed-form solution is that Z(x) is impossible to compute because it involves iterating all y, which is infinite. However, the form of the solution suggests a clever way of changing variables to bypass the computation of Z. To see that, first, we write r as a function of the policy:
Plugging this into the Bradley-Terry preference model, we can cancel out Z and make the preference modeling tractable:
The negative log-likelihood loss to fit the policy π to a given preference dataset D becomes:
🧠 What does the DPO update do? If we inspect deeper, the gradient update of DPO reads:
Intuitively, the gradient of the loss function LDPO increases the likelihood of the preferred completions yw and decreases the likelihood of dispreferred completions yl. Importantly, the examples are weighed by how much higher the implicit reward model rates the dispreferred completions, scaled by β, i.e, how incorrectly the implicit reward model orders the completions, accounting for the strength of the KL constraint.
—Text from [5]—
Implementing the DPO loss only takes a few lines of pseudo-code:
pi_logratios = policy_chosen_logps - policy_rejected_logps
ref_logratios = reference_chosen_logps - reference_rejected_logps
logits = pi_logratios - ref_logratios
loss = -logsigmoid(beta * logits)Here, the required inputs are the policy/reference chosen/rejected log probabilities of LLMs given data (yw,yl,x). The code is adapted from this repository.
❌ A drawback of DPO is its potential to rapidly overfit preference data, even with KL regularization. This limitation is highlighted in [7], and it stems from the nature of the sigmoid function in the Bradley-Terry model. Concretely, if p*(y ≻ y′ ) = 1, i.e., y is always preferred to y′, the DPO solution requires that π*(y′)/π*(y)=0, i.e. π*(y′)=0 regardless of the value of β. As preferences become more deterministic, which is common in empirical datasets due to the lack of data, the strength of the KL-regularization diminishes quickly, leading to the wrong estimation of π*(y′).
Alternative Preference Optimization
An alternative approach aiming for alignment training without relying on RL and reward models introduces a different objective function [6], which maximizes the margin between the log-likelihood of preferred and dispreferred outputs:
The method, known as Sequence-Likelihood Calibration (👉SLiC, [6]), introduces a new constrained term to maximize the likelihood of the optimized model on reference output, which serves a similar purpose of maintaining proximity between the optimized model and the reference one.
Implementing SLiC margin loss only modifies one line of the DPO pseudo-code:
loss = relu(1 - beta * logits) Here 𝛿 is parameterized to beta, i.e., 𝛿=1/beta.
👀 Here, we need to sample yref from the reference policy instead of computing the KL divergence term, which may be a limitation because sampling is often slower.
A more comprehensive perspective on preference learning, in which RLHF and DPO are special cases, introduces a Ψ-preference optimization (👉 Ψ-PO [7]) objective:
Depending on the choice of Ψ, we can recover the objective of RLHF coupled with the Bradley-Terry preference model. In particular, with Ψ(q) = log(q/(1 − q)) and p*(y ≻ y ′) = σ(r(y) − r(y ′ )):
Here and from now on, we exclude x to simplify the notations. As we can see, the RLHF objective is equivalent to the Ψ-PO objective, offset by a constant term. Using a similar derivation as in DPO, we can find the closed-form solution for the Ψ-PO objective as:
Although the derivation of Ψ-PO looks similar to DPO’s, the former offers a more generalized way to optimize the objective, which involves Ψ. Here, the closed-form solution cannot be computed exactly either (∝ means proportional to). However, we can go around this technical issue by division trick:
Following some math reformulation, we end up to solve for the equation:
👀 In DPO, the objective is equivalent to maximizing σ(h(y,y’)), which is so different from Ψ-PO.
The authors in [7] propose to use Ψ as an identity function, named 👉IPO, which simplifies the equation to solve:
This root-finding problem leads to the following mean-square error loss:
This loss can be proved to be equivalent to:
where I is drawn from a Bernoulli distribution with a mean of p*(y ≻ y’). This results in a naive estimation using samples of y and y’ such that if y is preferred to y’ I(y,y’)=1. On the other hand, I(y,y’)=0. This leads to the IPO loss for each pair of samples yw, yl ~D:
👀 The coefficient of 1/2 is present because each (yw, yl) pair represents four instances of the original loss, where yw and yl can be either y or y’. Due to the symmetry of h and the asymmetry of I, taking average results in the appearance of 1/2.
According to the authors, IPO is less overfitting to the preference data than DPO because:
In other words IPO, unlike DPO, always regularizes its solution towards πref by controlling the gap between the log-likelihood ratios log(π(yw)/π(yl)) and log(πref(yw)/πref(yl)), thus avoiding the over-fitting to the preference dataset.
—Text from [7]—
❌ Despite its theoretical rigorousness, IPO performance in practical benchmarks seems to be weaker than DPO, as showcased in this study. Implementing IPO is straightforward given the DPO code, which only replaces sigmoid with MSE:
loss = (logits - 1 / (2 * beta)) ** 2Self-Play Preference Optimization
Since LLMs are powerful models, they can be used to generate preference feedback for preference finetuning. In practice, researchers often use large LLMs like GPT-4 to generate preference datasets, where outputs for a given input from larger models are typically considered preferred over those from smaller ones. 🧠 Can we incorporate this concept into the direct preference optimization process to minimize the reliance on human preference data?
A recent paper (👉SPIN) answers YES to this question by providing a self-play alignment training that utilizes the output of the optimized LLM to construct preference data [8]. In the paper, the authors consider 2 LLMs and view one (the optimized LLM) as the main player ft+1 and the other (an old version of the optimized LLM) as the opponent player θt. Here, the timestep t denotes the optimization step. Then the objective function is designed such that the primary player ft+1 maximizes the expected gap between the target data distribution pdata and the opponent player's distribution pθt :
In essence, the main player aims to differentiate between the true data and the generated data from the opponent player. On the other hand, the opponent player’s goal is to generate outputs that are assigned high probability by the main player. In other words, it tries to fool the main player, which leads to the opponent player’s objective maximizing:
Combining with the usual KL-divergence loss to constrain the update of the opponent model not too far from its previous version, we arrive at finding the optimal opponent player:
👀 The self-play concept is very similar to GAN.
Given that we can model the optimal opponent player with an LLM with parameter θt+1, we can end up with a relationship between the opponent and the main player as:
As the name implies, in self-play, the main and opponent players are the same model, from different versions. The relationship defined above suggests a self-play update procedure as follows:
Given the relationship. to find θ for both players, we just need to optimize the main player objective, which is equivalent to minimizing the following loss:
This leads to the SPIN algorithm:
👀 The SPIN loss looks similar to DPO’s loss. Here are the differences:
SPIN does not require preference labels, it uses the old (weak) and the current (strong) model to generate output and assume the current output is preferred.
DPO necessitates that, at the instance level, yw is superior to yl. In contrast, SPIN requires that, at the distribution level, the target pdata should be distinguishable from the weak LLM pθ before it becomes strong.
❌ SPIN requires data generation for each iteration, which can be slow and expensive. Although it eliminates the need for preference data, it requires the supervised finetuning dataset. i.e., the ground truth y for x.
Finetuning with Rating Feedback
As demonstrated in earlier sections, the Bradley-Terry model has been extensively used in alignment training of LLMs. However, it is important to note that it is not the only preference model available. Another option is to utilize a different preference model, namely, the human value function proposed by Kahneman and Tversky:
The idea originates from the concept of loss aversion in behavioral economics, which observes that individuals tend to perceive losses as more significant than equivalent gains. It revolves around the notion that people assess their utility based on "gains" and "losses" relative to a specific reference point. This reference point varies among individuals and is relative to their unique circumstances.
Interestingly, previous approaches that utilize rewards (implicit or explicit) to model the human value function can be seen as variations of h, assuming that zref represents the reward for the dispreferred output. The figure below summarizes the idea:
All of these losses share similar characteristics of human value function:
1. the existence of a reference point that is added or subtracted to get the relative gain or loss
2. convexity of the value function in relative losses and concavity in gains (i.e., diminishing sensitivity the further you are from the reference point)
3. loss-aversion (a greater rate of change in utility in the loss regime)
—Text from [11]—
Given these observations, it seems more appropriate to directly utilize Kahneman and Tversky's human value function rather than other alignment losses because it may be easier to fit with the preference data, which is collected from real humans. 🧠 How can we employ the Kahneman and Tversky model for optimizing preferences in LLMs?
In [11], the authors propose one way to implement the human value function in aligning LLMs and call the method Kahneman-Tversky Optimization (👉 KTO). The approach suggests eliminating the use of pairs of labeled outputs for training. Instead, we only use a single output and compare it with an estimated zref. The authors also suggest using a sigmoid h instead of an exponential one for ease of optimization, resulting in the modified value function:
To simulate the two forms of the value for the gain and loss regime, the final function looks like this:
Here, we only need a label for one output y, and the labeler aims to answer the question: 🧠 is y desirable? In practice, this can be implemented as a like or dislike button to rate an output from the model. Given the form of the value function, we aim to minimize the following loss:
In practice, when implementing KTO, we need to estimate the KL term as:
where m is the batch size and z is the unrelated output (to create a clear gap between the reference and the value). For convenience, if y is desirable or chosen, z can be chosen as the rejected one and vice versa. The max operator is to ensure KL approximation is still greater than or equal to 0. Note that in training practice, we make use of the preference data as the rating data with yw as ydesriable and yl as yundersirable and thus, we can compute 2 KTO losses per (yw,yl,x). Concretely, we can implement KTO losses as follows:
chosen_KL = (policy_chosen_logps - reference_chosen_logps).mean().clamp(min=0)
rejected_KL = (policy_rejected_logps - reference_rejected_logps).mean().clamp(min=0)
chosen_logratios = policy_chosen_logps - reference_chosen_logps
rejected_logratios = policy_rejected_logps - reference_rejected_logps
chosen_loss = 1 - sigmoid(lambda_d * (chosen_logratios - rejected_KL))
rejected_loss = 1 - sigmoid(lambda_u * (chosen_KL - rejected_logratios))A major benefit of KTO is label efficiency. Instead of generating 2 outputs and asking for a comparison from humans as DPO does, KTO only generates 1 output and asks for a rating:
👀 As a result, with KTO, we can collect more data and labels from humans, which generally improves the performance of the aligned LLMs.
❌ KTO necessitates KL estimation, which demands a large batch size m for stable results. Consequently, this increases computational and memory requirements, making it less suitable for low-resource machines.
References
[1] Huang, Tzu-Kuo, Ruby C. Weng, Chih-Jen Lin, and Greg Ridgeway. "Generalized Bradley-Terry Models and Multi-Class Probability Estimates." Journal of Machine Learning Research 7, no. 1 (2006).
[2] Schoenauer, Marc, Riad Akrour, Michele Sebag, and Jean-christophe Souplet. "Programming by feedback." In International Conference on Machine Learning, pp. 1503-1511. PMLR, 2014.
[3] Christiano, Paul F., Jan Leike, Tom Brown, Miljan Martic, Shane Legg, and Dario Amodei. "Deep reinforcement learning from human preferences." Advances in neural information processing systems 30 (2017).
[4] Ouyang, Long, Jeffrey Wu, Xu Jiang, Diogo Almeida, Carroll Wainwright, Pamela Mishkin, Chong Zhang et al. "Training language models to follow instructions with human feedback." Advances in Neural Information Processing Systems 35 (2022): 27730-27744.
[5] Rafailov, Rafael, Archit Sharma, Eric Mitchell, Stefano Ermon, Christopher D. Manning, and Chelsea Finn. "Direct preference optimization: Your language model is secretly a reward model." arXiv preprint arXiv:2305.18290 (2023).
[6] Zhao, Yao, Misha Khalman, Rishabh Joshi, Shashi Narayan, Mohammad Saleh, and Peter J. Liu. "Calibrating sequence likelihood improves conditional language generation." arXiv preprint arXiv:2210.00045 (2022).
[7] Azar, Mohammad Gheshlaghi, Mark Rowland, Bilal Piot, Daniel Guo, Daniele Calandriello, Michal Valko, and Rémi Munos. "A general theoretical paradigm to understand learning from human preferences." arXiv preprint arXiv:2310.12036 (2023).
[8] Chen, Zixiang, Yihe Deng, Huizhuo Yuan, Kaixuan Ji, and Quanquan Gu. "Self-play fine-tuning converts weak language models to strong language models." arXiv preprint arXiv:2401.01335 (2024).
[9] Bai, Yuntao, Saurav Kadavath, Sandipan Kundu, Amanda Askell, Jackson Kernion, Andy Jones, Anna Chen et al. "Constitutional ai: Harmlessness from ai feedback." arXiv preprint arXiv:2212.08073 (2022).
[10] Lee, Harrison, Samrat Phatale, Hassan Mansoor, Kellie Lu, Thomas Mesnard, Colton Bishop, Victor Carbune, and Abhinav Rastogi. "Rlaif: Scaling reinforcement learning from human feedback with ai feedback." arXiv preprint arXiv:2309.00267 (2023).
[11] Ethayarajh, Kawin, Winnie Xu, Niklas Muennighoff, Dan Jurafsky, and Douwe Kiela. "KTO: Model Alignment as Prospect Theoretic Optimization." arXiv preprint arXiv:2402.01306 (2024).







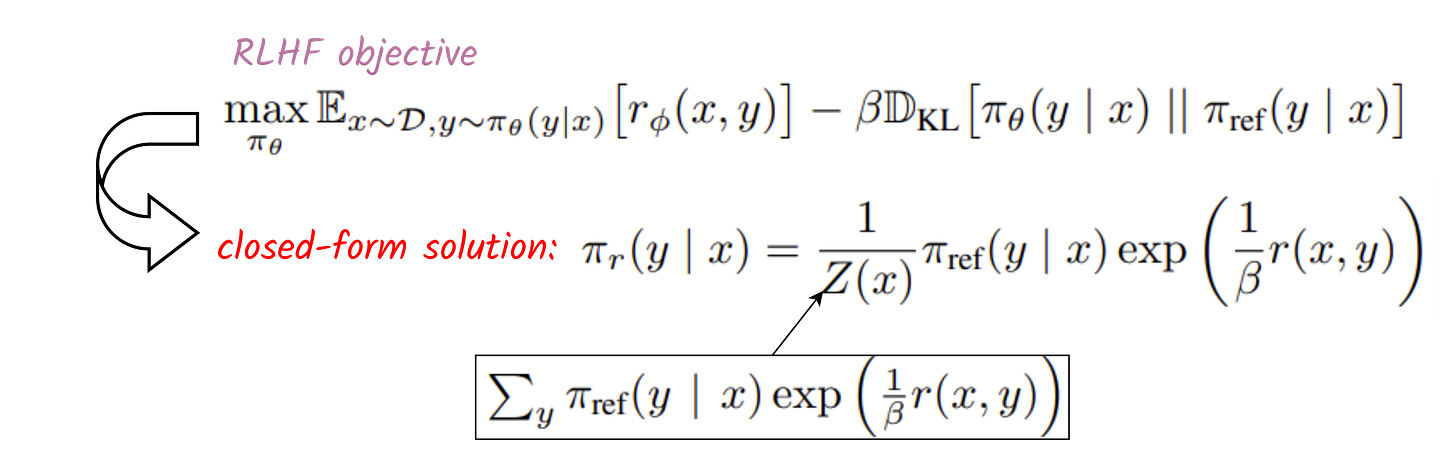
















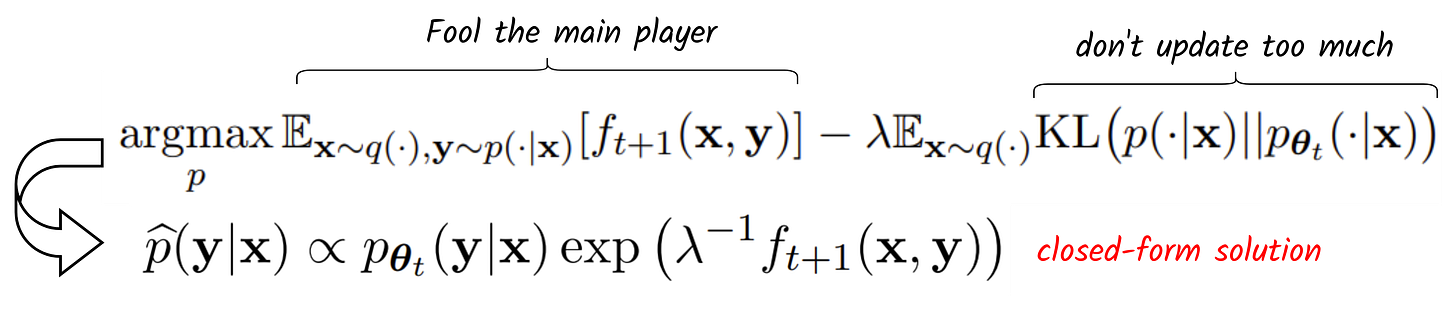








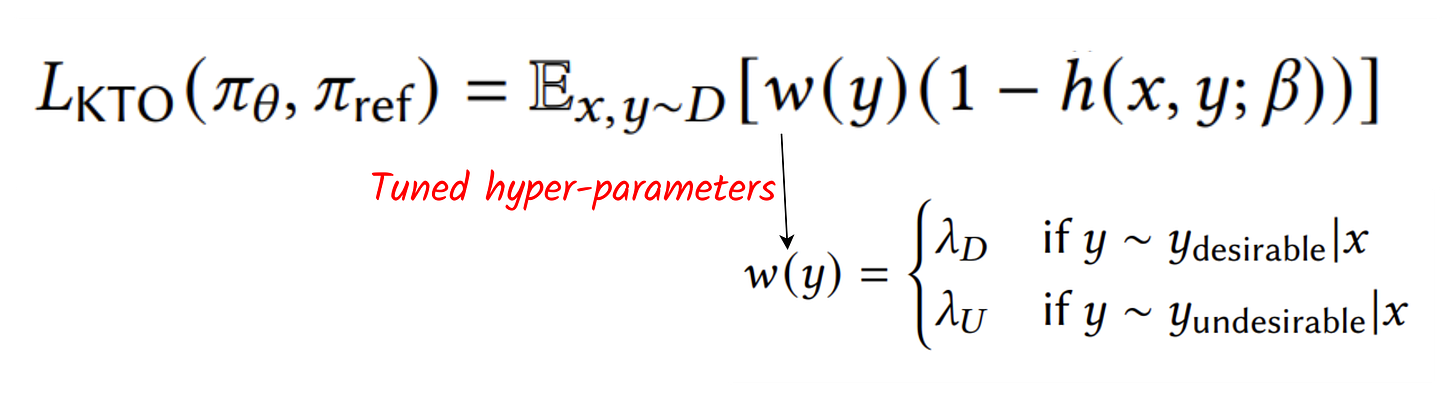


Regarding alignment, it's like adjusting my bike gears perfecly.