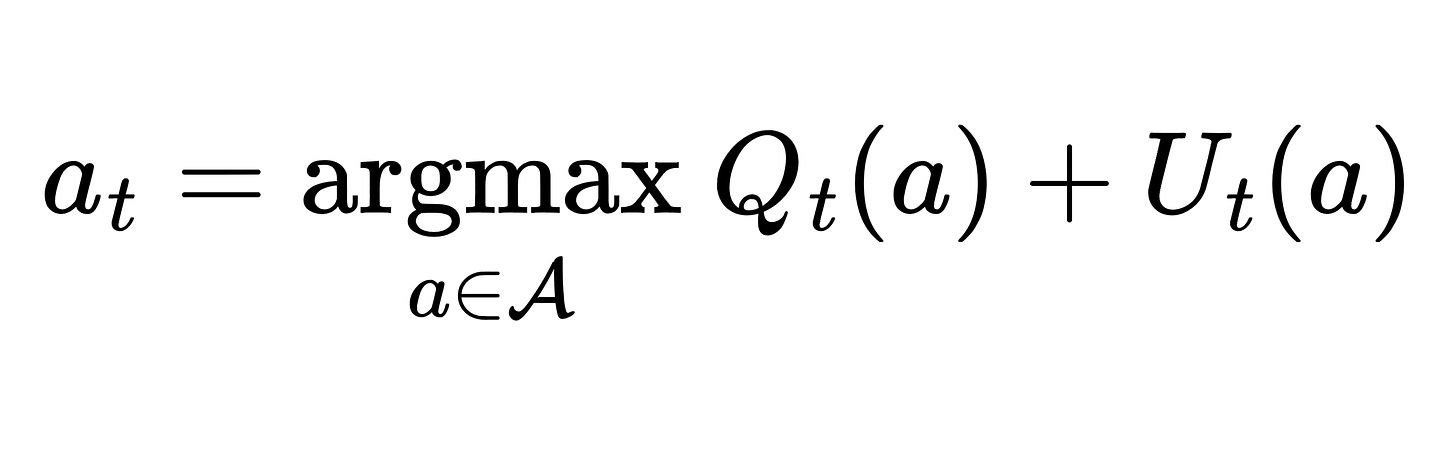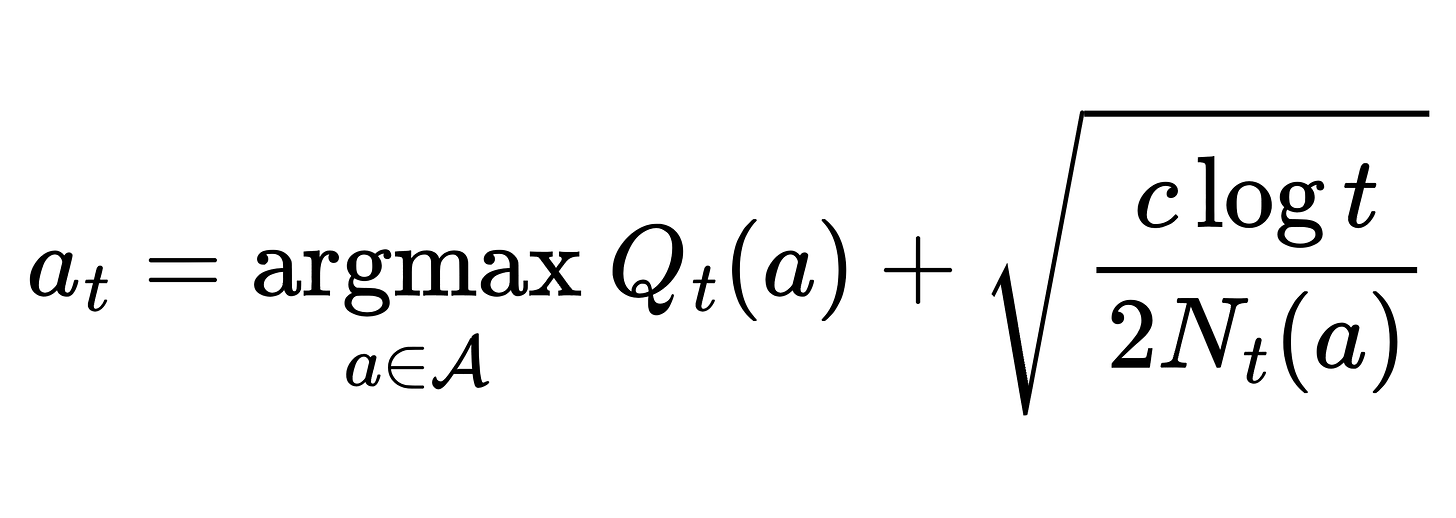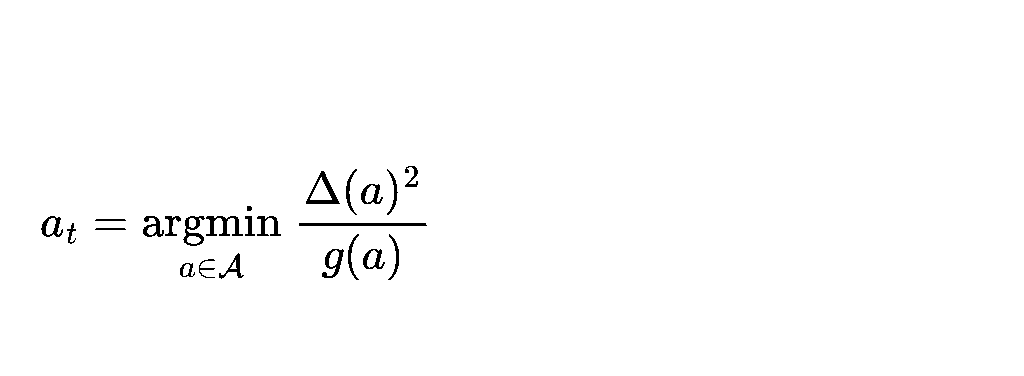Table of Content
Exploration in Reinforcement Learning
In reinforcement learning (RL), an agent interacts with the environment, taking actions a, receiving a reward r, and moving to a new state s. The agent is tasked with maximizing the accumulated rewards or returns R over time by finding optimal actions (policy).
To learn, the agent experiments with various actions and observes their consequences. It starts by exploring the environment with random actions and then determining which actions bring good and bad rewards. Here, we will not focus on how the agent can learn given his experiences in the environment. Rather, we are curious about the exploration strategies that trigger the learning. It comes as no surprise that not all explorations are equal. Consider the illustration below, the purely random exploration (left figure), as often used in Q-learning, is inefficient, requiring countless interactions for the agent (yellow circle) to reach the goal (red diamond). Conversely, a strategic sweep of all possible areas (right figure) can significantly save time and effort for the agent in locating the goal. 🧠 What makes a good exploration?
Classic Explorations
These approaches were developed before the deep learning era. They were primarily focused on the multi-arm bandit problem, a special branch of reinforcement learning where the state can be overlooked. Many of these approaches come with theoretical guarantees under certain assumptions that are not easily extended to complicated environments with high-dimensional state space.
ε-greedy
ε-greedy is the simplest exploration strategy that works (in theory). Unfortunately, it heavily relies on pure randomness and biased estimates of action values Q, and thus is sample-inefficient in practice. It is like flipping a coin when making decisions. We often go with what we assume is best, but sometimes, we take a random chance to explore other options. This is one example of an optimistic strategy. Formally, it reads:
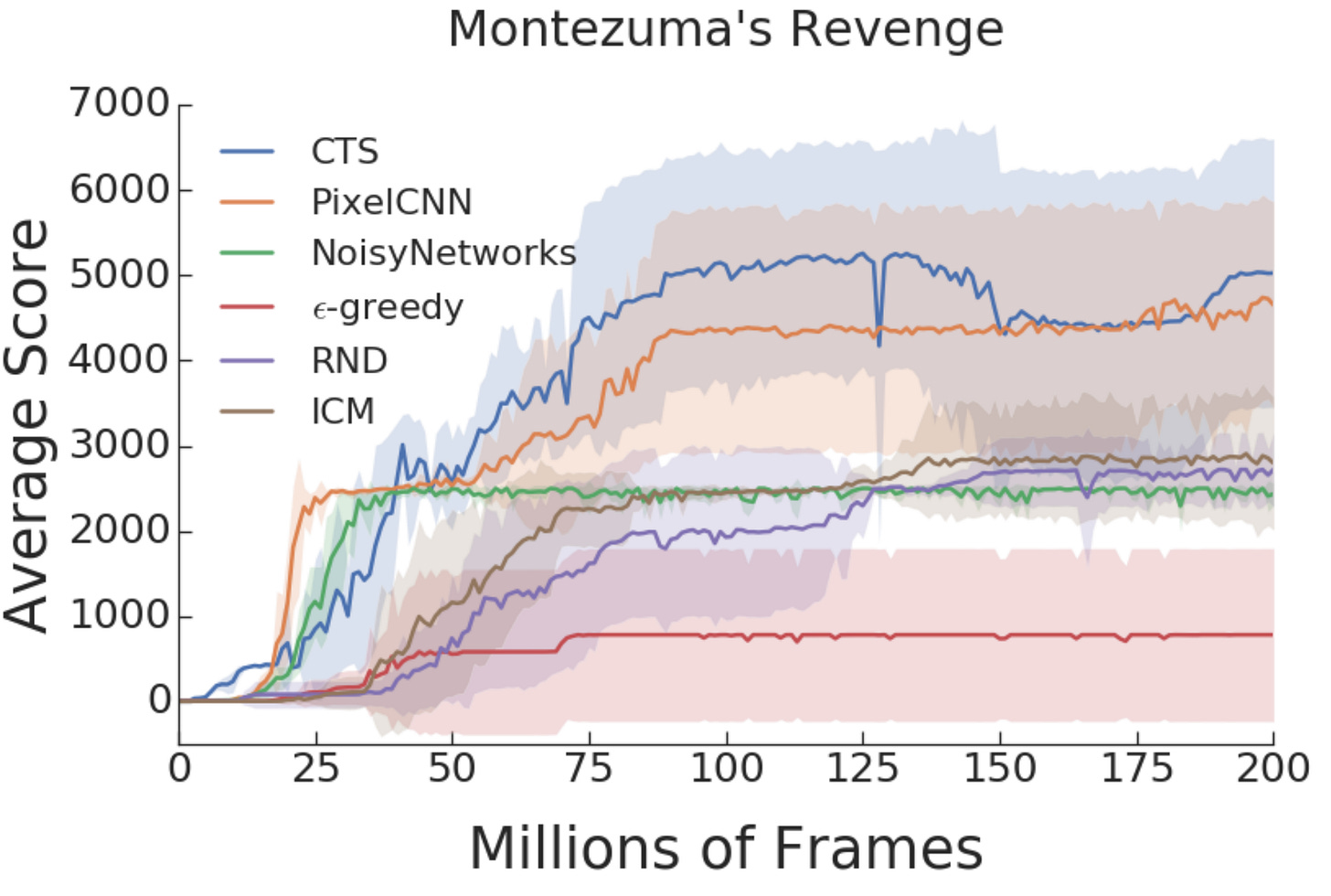
where Q is the estimated value for taking action a. Here, we use the action value (ignoring the state), but it can be applied to the state-action value in normal RL. Despite its simplicity, ε-greedy is still widely used in modern RL such as DQN and often works well in dense-reward environments. However, for sparse reward environments, ε-greedy struggles to explore, as evidenced in Montenzuma’s Revenge.
👀 It is not surprising why this strategy might struggle in real-world scenarios: being overly optimistic when your estimation is imprecise can be risky. It may lead to getting stuck in a local optimum and missing out on discovering the global one with the highest returns.
Upper Confidence Bound (UCB)
One way to address the problem of over-optimism is to consider the uncertainty of the estimation. Intuitively, we do not want to miss an action with a currently low estimated value and high uncertainty, as it may possess a higher value. The following formula (UCB strategy) reflects this intuition:
where Ut is the estimated uncertainty of taking action a at timestep t. Ut is also known as the upper confidence for the true action value Q* if we can guarantee that
If the inequality is true, the error of taking action a according to UCB will be reduced. It can be proven that the error, in the form of regret, follows a logarithmic asymptotic pattern compared to the linear regret of ε-greedy, yet we will not go into the details here. Rather, we focus on: 🧠 How to ensure the inequality?
To find Ut , we use Hoeffding’s Inequality. By treating X as the return R(a) and estimating Q(a) as the sample mean, we have:
In simple terms, to guarantee the true Q* within a tight confidence bound, the right-hand side (RHS) should be maintained minimal, implying that the uncertainty (U) is inversely proportional to the square root of the number of trials (N). In essence, as we gather more trials (N increases), the uncertainty is allowed to decrease, leading to a reduction in the bound. If we denote the probability bound (RHS) as p, we can solve for U:
In practice, we can reparameterize p as t-c and tune c as a hyperparameter. This leads to the classic UCB strategy:
👀 While UCB does not involve explicit randomness, the action selection is not confined to a strictly greedy approach based solely on Q estimation. Implicitly, with a large value of the exploration-exploitation trade-off parameter c, the chosen action is more likely to deviate from the greedy action, leading to increased exploration.
Thompson Sampling
When additional assumptions about the reward distribution are available, we can calculate the probability of each action being optimal. Consequently, an action can be chosen based on the probability that it is optimal (probability matching strategy). Formally, the probability of choosing action a is:
Thompson sampling is one way to implement the probability matching strategy, and can be understood in a Bayesian setting as follows:
Assume the reward follows a distribution p(r|a, θ) where θ is the parameter whose prior is p(θ)
Given the set of past observations Dt is made of triplets {(ai, ri)|i=1,2..,t}, we update the posterior using Bayes rule:
Given the posterior, we can estimate the action value
Then, we can compute the probability of choosing action a
In practice, there is no need to compute the integral explicitly; it suffices to sample one θ and use it to calculate the probability of choosing action a. This aligns with the strategy of selecting a as the best option based on the current estimated action value using θ. The whole process is summarized in the following algorithm, extended to the contextual multi-arm bandit with additional context input x.
Information Gain
Information Gain (IG) measures the change in the amount of information (measured in entropy H) of a latent variable, often referring to the parameter of the model θ after seeing observation (e.g., reward r) caused by some action a. A big drop in the entropy means the observation makes the model more predictable and less uncertain, giving us valuable information from the action a that leads to the observation. Formally, we have:
In essence, our goal is to find a harmony between minimizing expected regret in the current period and acquiring new information about the observation model. The intuition suggests this objective:
Overall, this approach demonstrates better results compared to Thompson Sampling and UCB, in terms of minimizing cumulative regret, as shown in the figure below:

👀 While classical exploration approaches have rigorous theoretical foundations, they are not without their limitations:
❌ Scalability Issues: Most are specifically designed for bandit problems, and thus, they are hard to apply in large-scale or high-dimensional problems (e.g., Atari games), resulting in increased computational demands that can be impractical.
❌ Assumption Sensitivity: These methods heavily rely on specific assumptions about reward distributions or system dynamics, limiting their adaptability when assumptions do not hold.
❌ Vulnerability to Uncertainty: They may struggle in dynamic environments with complex reward structures or frequent changes, leading to suboptimal performance.
Primal Exploration in Deep Reinforcement Learning
Entropy Maximization
In the era of deep learning, neural networks are used for approximating functions, including parameterizing value and policy functions in RL. While adopting ε-greedy is a simple exploration strategy for value-based deep RL like DQN, it becomes less straightforward for policy gradient methods. To address this, an entropy loss term is introduced in the objective function to penalize overly deterministic policies. This encourages diverse exploration, avoiding suboptimal actions by maximizing the bonus entropy loss term in policy gradient methods.
👀 Key papers leveraging this loss, such as A3C and PPO, assert enhanced exploration by discouraging premature convergence to suboptimal deterministic policies. Nevertheless, adding an extra loss is a double-edged sword—it enhances exploration but may also impede the optimization of other losses, especially the main objective. Moreover, the entropy loss does not enforce different level of exploration for different tasks. This is impractical since intuitively, certain tasks, particularly those with sparse rewards, may require more exploration than others.
Noisy Networks
Another method to add randomness to the policy is to add noise to the weights of the neural networks [5]. For example, a noisy feedforward layer of a neural network is depicted below:

The noise variables can be sampled independently from a zero-mean Gaussian distribution, resulting in the number of noise variables equalling the number of trainable parameters. Alternatively, they can be factorized into the product of two noises, each sampled from a zero-mean Gaussian:
where f is a real-valued function that scales the original noises. Throughout training, noise samples are drawn and added to the weights for both forward and backward propagation. Interestingly, a similar concept was introduced around the same period in a concurrent study [6]. Both [5] and [6] received acceptance at ICLR 2018.
Noisy layers can be used to replace feedforward layers in the value network (DQN) and policy network (A3C). As the parameters of the noisy layer are trainable, it can dynamically adjust the exploration level to suit the task. For example, tasks with minimal exploration should feature small µ and σ, while tasks requiring more exploration should exhibit the opposite, as depicted below:
👀 Although Noisy Networks can vary exploration degree across tasks, adapting exploration at the state level is far from reachable. Certain states with higher uncertainty may require more exploration, while others may not.
🧠 How to know which state should be explored? Addressing this question will necessitate more sophisticated approaches, which will be covered in part 2 of my article.
References
[1] Sutton, Richard S., and Andrew G. Barto. Reinforcement learning: An introduction. MIT Press, 2018.
[2] Taïga, Adrien Ali, William Fedus, Marlos C. Machado, Aaron Courville, and Marc G. Bellemare. "Benchmarking bonus-based exploration methods on the arcade learning environment." arXiv preprint arXiv:1908.02388 (2019).
[3] Chapelle, Olivier, and Lihong Li. "An empirical evaluation of Thompson sampling." Advances in neural information processing systems 24 (2011).
[4] Russo, Daniel, and Benjamin Van Roy. "Learning to optimize via information-directed sampling." Advances in Neural Information Processing Systems 27 (2014).
[5] Fortunato, Meire, Mohammad Gheshlaghi Azar, Bilal Piot, Jacob Menick, Ian Osband, Alex Graves Vlad Mnih, Remi Munos Demis Hassabis Olivier Pietquin, Charles Blundell, and Shane Legg. "Noisy Networks for Exploration." arXiv preprint arXiv:1706.10295 (2017).
[6] Plappert, Matthias, Rein Houthooft, Prafulla Dhariwal, Szymon Sidor, Richard Y. Chen, Xi Chen, Tamim Asfour, Pieter Abbeel, and Marcin Andrychowicz. "Parameter space noise for exploration." arXiv preprint arXiv:1706.01905 (2017).