Rethinking Memory: A Unified Linear Approach for Mindful Agents

Stable Hadamard Memory: Revitalizing Memory-Augmented Agents for Reinforcement Learning (ICLR 2025)

Jan 22, 2025

In reinforcement learning (RL), memory isn't just a bonus—it's a necessity. When agents operate in environments where they can't directly see everything they need (think navigating a maze), they must rely on memory to make decisions. This is where things get tricky: most current memory models fail under the weight of complex, long-term tasks where agents must selectively retain and erase memories based on relevance.

👀 In this setting, it is surprising that simple recurrent memory such as RNN, LSTM and GRU outperforms powerful memory models such as Transformer and attention-based memories.

Enter the 👉Stable Hadamard Memory (SHM [1]). This new memory framework promises to revolutionize how RL agents manage their memories by solving longstanding problems with stability, flexibility, and scalability. Let’s dive into how it works, why it matters, and what the experiments reveal.

Table of Content

Octopuses possess impressive long-term memory, allowing them to remember solutions to problems for months. 🧠 They're also highly adaptable learners, constantly adjusting their strategies.

The Problem: Memory in RL is Hard

RL agents learn by interacting with their environment, acting, and receiving rewards. However, many real-world scenarios present significant challenges:

Partial Observability: Often, the current observation doesn't reveal the complete state of the environment. Imagine a robot navigating a maze where only a limited portion is visible. Past observations are crucial to understanding the overall layout and make informed decisions.
Long-Term Dependencies: Rewards may be delayed, and the consequences of an action might not be immediately apparent. For example, a seemingly insignificant early move can have profound long-term effects in a complex game.
Dynamic Environments: The world is constantly changing. Agents need to adapt their understanding and adjust their behavior based on new information and evolving conditions.

Why Need Memory?

RL agents often need to remember past experiences. This is especially crucial in situations where the current observation doesn't reveal the full picture (like in a partially observed environment). Imagine a robot navigating a maze. It needs to remember where it has been to avoid going in circles. Or think of a game like chess – past moves heavily influence the current situation. Without memory, these tasks become nearly impossible.

However, giving an RL agent memory is tricky. Existing approaches face several hurdles:

Information Overload: Agents need to selectively remember relevant information while discarding irrelevant details. This is crucial for efficient learning and decision-making.
Catastrophic Forgetting: As new information is acquired, older memories can be overwritten or "forgotten," hindering long-term performance.
Stability Issues: Many memory-augmented models can suffer from instability, leading to erratic behavior and poor performance.

Memory Operations

The agent needs a "memory" to store and retrieve relevant information. In our case, this memory can be represented by a matrix called M.

Reading from Memory:

To access information from this memory, the agent uses a "query network" (think of it as a question). This network takes the current situation (x_t) and translates it into a "query vector" (q). This query vector then interacts with the current memory matrix M_t to retrieve a relevant piece of information (h_t). This retrieved information is crucial for the agent to decide what action to take (policy) or how good a particular situation is (value):

\(h_t=M_tq(x_t)\)

Writing to Memory:

Now, the real challenge lies in how the agent "writes" information into this memory. Just like a student needs to learn and store new information effectively, the agent needs a mechanism to update its memory based on its experiences. This process is governed by an "update function" (f):

\(M_t=f(M_{t-1},x_t)\)

This equation essentially means that the current memory state (M_t) is determined by the previous memory state (M_t-1) and the current situation (x_t). The update function defines how new information is integrated into the existing memory, ensuring that the agent can efficiently and accurately retrieve information when needed.

In simpler terms:

The agent learns by storing experiences in its memory.
To use this memory, the agent "asks" a question (query) and retrieves relevant information.
The key is to effectively update the memory with new experiences, which is governed by the update function.

Why This Matters?

The Issues of Long-term Memorization. Current methods for giving agents memory, especially those inspired by deep learning, often struggle in these dynamic situations. Complex environments overwhelm agents, forcing them to prioritize information. Attention mechanisms, while powerful, can be slow and data-hungry, struggling to identify crucial memories. Sparse rewards further complicate the learning process, making it difficult to determine the value of stored information. In some cases, simpler RNNs might outperform attention-based and specialized RL models due to their efficiency and stability.

Model-free RNN agents outperform other methods. Source: [2].

👀 In RNNs, the memory update function is the RNN cell where M_t is just the hidden state vector of the RNN.

However, RNNs exhibit a significant limitation: a short memory span. This means they struggle to remember information from distant past events in the sequence. Furthermore, RNNs are inherently sequential, hindering their ability to leverage parallel processing techniques. This sequential processing can significantly slow down both training and inference, often resulting in longer processing times compared to Transformer models.

Overcoming these challenges is critical for advancing the capabilities of RL agents in real-world applications:

Robotics: Robots need memory to navigate complex environments, interact with humans, and perform tasks that require long-term planning.
Healthcare: AI-powered medical diagnosis systems can benefit from memory to learn from patient histories, identify patterns, and provide personalized treatment plans.
Autonomous Systems: Self-driving cars and drones require memory to understand traffic patterns, anticipate potential hazards, and make safe and efficient navigation decisions.

The Solution: Stable Hadamard Memory (SHM)

At the heart of SHM is the Hadamard Memory Framework (HMF), a versatile model for memory updates that support calibration and update.

Calibration: This process determines which parts of the existing memory should be strengthened or weakened. Imagine it as fine-tuning the importance of past experiences.
Update: This step introduces new information into the memory. Think of it as adding new entries to your journal.

Stable Hadamard Framework (SHF)

Memory M is represented as a square matrix. At any timestep t, the memory evolves according to the update rule:

\(M_t = M_{t-1} \odot C_\theta(x_t) + U_\phi(x_t) \)

Here’s what the components mean:

Calibration Matrix C_θ(x_t): Dynamically adjusts memory elements based on the current input x_t strengthening or weakening specific parts.
Update Matrix U_ϕ(x_t): Encodes new information into memory.
Hadamard Product ⊙: Performs element-wise operations, avoiding interference between unrelated memory cells.

The framework enables the calibration matrix C and the update matrix U to be parameterized functions of the input x_t, ensuring adaptive and context-aware memory updates.

Why Hadamard Product?

The paper specifically chooses the Hadamard product for two key reasons:

Efficiency: It operates on each memory element individually, making it computationally efficient.
Preservation of Information: It avoids mixing information from different memory cells during calibration and update, ensuring the integrity of stored information.

The Update Matrix

Inspired by fast weight systems [3], the update matrix is defined as:

\(U_\phi(x_t) = \eta_\phi(x_t) [v(x_t) \otimes k(x_t)] \)

v(x_t) and k(x_t): Trainable neural networks that generate value and key representations, respectively.
η_ϕ(x_t): A parameterized gating function that controls the degree of memory update at each step, implemented as a neural network with sigmoid activation.

The Calibration Matrix

The calibration matrix C_t is critical in forgetting irrelevant details and reinforcing crucial memories.

👀 By carefully designing the calibration matrix, we can selectively "forget" irrelevant information and "reinforce" crucial memories.

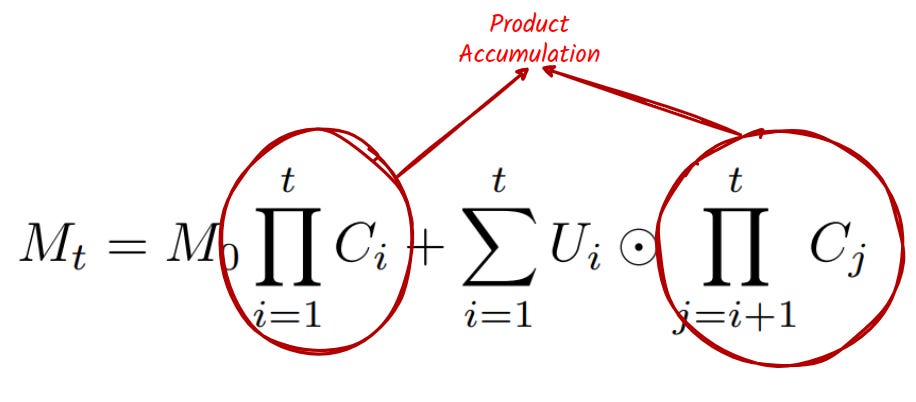
We can derive the explicit form of the memory with the calibration and update matrix as follows:

\(M_t = M_0 \prod_{i=1}^{t} C_i + \sum_{i=1}^{t} U_i \odot \prod_{j=i+1}^{t} C_j \)

In this form, we can realize one of the most exciting aspects of the Hadamard Memory Framework is its inherent parallelism thanks to its 👉computing linearity. This means we can leverage the power of parallel computing to significantly speed up the memory processing.

Parallel Product Calculation: The core of the memory update involves a series of products. Leveraging prefix product algorithms, they can be performed simultaneously, or "in parallel." This dramatically reduces the time required for this step, achieving a remarkable time complexity of O(log t).
Parallel Summation: Not only the products but also the subsequent summation of these products can be executed in parallel. This further accelerates the overall processing speed.
Element-wise Operations: The beauty of the framework lies in its reliance on element-wise operations (like the Hadamard product). This allows for massive parallelization across the entire memory dimensions, leading to a significant performance boost.

Thanks to these parallel processing capabilities, the Hadamard Memory Framework achieves a total time complexity of O(log t). This translates to significantly faster memory updates compared to traditional sequential approaches like RNNs.

Why Calibration is Essential

In reinforcement learning, memory isn’t just about storing information—it’s about keeping the right information while discarding the rest. This is where calibration comes into play. Without calibration, the memory system risks becoming either too rigid, holding onto irrelevant data indefinitely, or too volatile, forgetting valuable context too soon. Let’s explore why calibration C_t is a game-changer compared to a static, uncalibrated approach (C_t=1).

What Happens Without Calibration?

If C_t=1 for all timesteps, the memory evolves simply by adding new updates without selectively weakening or enhancing previous entries. Over time, this creates two significant problems:

Irrelevant Information Overload: The memory retains all past data, regardless of its current importance. For example, imagine an agent tasked with navigating a room:
- It encounters a color code (important for unlocking a door later).
- Then, it picks apples (less important for its goal).
Without calibration, the memory retains every detail about the apples, making it harder to retrieve the critical color code when needed.
Inflexibility: Fixed memory updates can’t adapt to changing needs. If the agent later needs to remember the apple task (say it becomes relevant again), uncalibrated memory won’t effectively recall it.

How Calibration Solves This

The calibration matrix C_t allows the memory to dynamically adjust what’s remembered and forgotten, based on the context at each timestep t. Here’s how:

Forgetting Irrelevant Details: Calibration ensures that unimportant details—like the apple-picking task—are gradually weakened in memory. Mathematically, U_i⊙∏_j=i+1:tC_j≈0 for irrelevant timesteps i. This makes retrieving critical data (like the color code) easier.
Reinforcing Important Memories: If a previously irrelevant timestep i becomes important again, calibration strengthens its contribution, ensuring Ui⊙∏_j=i+1:t′Cj≠0 when needed.

An Intuitive Analogy: Think of calibration as a highlighter for your memory. Imagine reading a long book:

❌ Without calibration, every word is stored with equal weight. Trying to recall key points later would be like searching for a needle in a haystack.

✅ With calibration, the highlighter lets you emphasize the essential sections (like the main plot points) and fade out less relevant details (like minor background descriptions).

👀 Do you realize that SHF is very generic. Special cases of SHF includes: (1) SSM: M_t, C_t, and U_t are vectors; (2) Linear Attention: C_t=1; (3) mLSTM: C_t is a scalar. See more special cases of SHF at the end of the blog post.

Designing Stable Calibration: The Core of Stable Hadamard Memory

At the heart of SHF lies the calibration matrix C_t. This matrix ensures that memory updates remain stable, effective, and context-aware, even over long sequences of steps. Let’s break this down step by step, showing how the design of C_t balances adaptability and stability in reinforcement learning.

Why Care About Stability?

Looking at the explicit form of the memory update, we can see the cumulation of calibration through the accumulated product of C.

Therefore, memory updates can face two major pitfalls:

Exploding or Vanishing Gradients: Without proper bounds, the cumulative effect of updates can grow too large (exploding) or shrink to zero (vanishing). This disrupts learning.
Overlapping Dependencies: If memory updates at one timestep are too closely tied to updates at another, the system loses flexibility and struggles with new contexts.

A Dynamically Bounded Calibration Matrix

Stable Hadamrad Memory (SHM) introduces a special calibration matrix C_t defined as:

\(C_\theta(x_t) = 1 + \tanh(\theta_t \otimes v_c(x_t)) \)

Here’s how it works:

θ_t: Trainable parameters that are randomly selected for each timestep.
v_c(x_t): A mapping function (e.g., a linear transformation) that converts the input context x_t into a memory-compatible representation.
tanh()⁡: Ensures that the values of C_t are bounded between 0 and 2

This dynamic design keeps updates stable by ensuring that the cumulative product of calibration matrices is bounded:

\(\mathbb{E}\left[\prod_{t=1}^T C_t\right] \approx 1 \)

This means the memory remains well-calibrated, neither exploding nor disappearing, even as the number of timesteps T grows.

Why Randomly Select θ_t?

Randomly sampling θ_t breaks dependencies between timesteps, reducing correlations and enabling the memory to adapt to new inputs. Think of it as adding a degree of randomness that helps the system focus on the task at hand, instead of being overly influenced by past updates.

Proposition 5 in the paper mathematically supports this idea by showing that random sampling minimizes the Pearson correlation between timesteps:

\(\rho(u_t^m v_t^k, u_{t'}^m v_{t'}^k) \leq \rho(v_t^k, v_{t'}^k) \)

This ensures that the calibration matrix adjusts independently for each timestep, promoting that the cumulative product of calibration matrices is bounded.

Summary of Practical Benefits

✅ Dynamic Memory Updates: C_t adjusts based on the current context x_t enabling adaptive forgetting and prioritization of critical information.

✅ Numerical Stability: By bounding C_t, SHM prevents gradients from exploding or vanishing.

✅ Efficient Training: The use of Hadamard products enables parallel training and inference

The diagram below summarizes the architecture and memory update operation of the SHM:

SHM memory update. In this example, the memory size is H=5. The memory parameter θ set size is L=4.

Experiments That Speak Volumes

Meta-Reinforcement Learning

Meta-reinforcement learning (Meta-RL) challenges agents to adapt to ever-changing environments with varying tasks and goals. These scenarios demand memory systems that can generalize across tasks, remember critical past information, and adapt to unseen situations.

In SHM's evaluation, two Meta-RL environments were used: Wind and Point Robot.

Wind: The agent's goal is fixed but affected by random "wind" forces that shift its trajectory.
Point Robot: The goal changes between episodes, requiring the agent to adapt.

Rewards were sparse, with the agent only rewarded for reaching a goal within a small radius. SHM and baseline models were tested in two modes:

Easy Mode (50 training tasks, 150 testing tasks): SHM achieved near-optimal success, outperforming other models by 20-50%.
Hard Mode (10 training tasks, 190 testing tasks): SHM maintained a ~20% performance lead, learning faster and adapting earlier than baselines like GRU and FFM.

These results highlight SHM’s strength in environments where efficient adaptation and task generalization are essential.

Long-Term Credit Assignment

Some tasks, like connecting distant events, require agents to retain and recall information over extended timeframes. Visual Match and Key-to-Door exemplify this:

Visual Match: Agents observe a color code early on, pick apples for intermediate rewards, and match the code to a door for the final reward.
Key-to-Door: The agent collects a key in one phase, performs unrelated tasks, and later uses the key to open a door.

SHM dominated these tasks:

In Visual Match (250 and 500 steps), SHM was the only model to achieve perfect success rates, while FFM reached 77% (250 steps) and 25% (500 steps).
In Key-to-Door, SHM demonstrated similarly high success rates, while other models, including GPT-2, showed little to no learning.

This success is attributed to SHM's calibration mechanism, which dynamically forgets irrelevant details (like apple-picking events) while preserving critical information (like the color code or key location).

POPGym Benchmarks

POPGym is the ultimate testbed for memory models, offering ultra-long tasks like Autoencode, Battleship, and RepeatPrevious that require agents to memorize and use information across 1,024 steps.

SHM outperformed state-of-the-art memory models (e.g., GRU, FFM) by 10-12% on average in the most challenging tasks:

RepeatPrevious: Only SHM consistently showed learning in the Medium/Hard modes.
Autoencode: SHM excelled across Easy/Medium tasks, proving its scalability in ultra-long scenarios.

While SHM's training time was slightly longer (1.9ms per batch vs. 1.6ms for GRU), the trade-off was well worth the superior performance in these memory-intensive environments.

Ablation Study: Why Random Calibration Works

The study explored the impact of different calibration strategies for C_t, showing that randomly selected θ_t offers the best balance of stability and adaptability:

Fixed calibration matrices (C=1 or Fixed θ_t) suffered from gradient vanishing issues, limiting performance.
Random θ_t minimized timestep dependencies, keeping the cumulative product ∏C_t close to 1 and maintaining stable gradient propagation.

Appendix

Memory writing mechanisms have evolved significantly, from simple additive updates to sophisticated architectures inspired by neuroscience and computer science. The Stable Hadamard Framework (SHF) unifies these diverse approaches under a single umbrella, showing that many existing memory models are just special cases.

The Foundations: Hebbian Learning

The simplest memory writing rule comes from Hebbian learning [3]:

\(M_t = M_{t-1} + x_t \otimes x_t \)

Here, ⊗ represents the outer product, storing new information by directly adding it to the existing memory. While straightforward, this method lacks adaptability—it cannot prioritize or forget information, making it impractical for dynamic environments.

Fast Weight Systems

Later, researchers introduced fast weight memory [4], which introduces weighted updates:

\(M_t = M_{t-1} \lambda + \eta g(M_{t-1}, x_t) \otimes g(M_{t-1}, x_t) \)

g: A non-linear function mapping memory and input.
λ, η: Hyperparameters controlling decay and learning rates.

This method allows some adaptability but still suffers from recursive computation, which can slow down training.

Neural Turing Machines and Differentiable Neural Computers

Computer-inspired architectures like the Neural Turing Machine (NTM [5]) and Differentiable Neural Computer (DNC [6]) added mechanisms for selective erasure and writing:

\(M_t = M_{t-1} \odot (1 - w(M_{t-1}, x_t) \otimes e(M_{t-1}, x_t)) + w(M_{t-1}, x_t) \otimes v(M_{t-1}, x_t) \)

w, e, v: Functions controlling weights, erasure, and values.
⊙: Hadamard (element-wise) product.

While powerful, these systems rely heavily on recursive computation and complex non-linear functions, making them computationally intensive.

Simplified Linear Transformers

To address computational challenges, Linear Transformers [7] simplified the update process:

\(M_t = M_{t-1} + v(x_t) \otimes \frac{\phi(k(x_t))}{\sum_t \phi(k(x_t))} \)

ϕ: An activation function.
k, v: Functions generating keys and values.

This approach focuses on computational efficiency but sacrifices flexibility, limiting its generalization capabilities.

Neuroscience-Inspired Fast Forgetful Memory

Inspired by the brain’s ability to forget, Fast Forgetful Memory (FFM [8]) introduced parallel updates:

\(M_t = M_{t-1} \odot \gamma + v(x_t) \otimes 1^\top \odot \gamma^{t-n} \)

γ: A trainable forgetting factor.

FFM balances forgetting and updating but does not address long-term stability issues comprehensively.

Matrix-Based LSTMs (mLSTM)

The recent matrix-based LSTM (mLSTM [9]) further builds on gating mechanisms:

\(M_t = f(x_t) M_{t-1} + i(x_t) v(x_t) \otimes k(x_t) \)

f, i: Forget and input gates controlling memory flow.

While effective, mLSTM does not guarantee stability calibration.

References

[1] Le, Hung, Kien Do, Dung Nguyen, Sunil Gupta, and Svetha Venkatesh. "Stable Hadamard Memory: Revitalizing Memory-Augmented Agents for Reinforcement Learning." ICLR, 2025.

[2] Ni, Tianwei, Benjamin Eysenbach, and Ruslan Salakhutdinov. "Recurrent Model-Free RL Can Be a Strong Baseline for Many POMDPs." In International Conference on Machine Learning, pp. 16691-16723. PMLR, 2022.

[3] Donald Olding Hebb. The organization of behavior: A neuropsychological theory. Psychology Press, 2005

[4] Jimmy Ba, Geoffrey E Hinton, Volodymyr Mnih, Joel Z Leibo, and Catalin Ionescu. Using fast weights to attend to the recent past. In Advances in Neural Information Processing Systems, pages 4331–4339, 2016.

[5] Alex Graves, Greg Wayne, and Ivo Danihelka. Neural Turing machines. arXiv preprint arXiv:1410.5401, 2014.

[6] Alex Graves, Greg Wayne, Malcolm Reynolds, Tim Harley, Ivo Danihelka, Agnieszka GrabskaBarwinska, Sergio G ´ omez Colmenarejo, Edward Grefenstette, Tiago Ramalho, John Agapiou, ´ et al. Hybrid computing using a neural network with dynamic external memory. Nature, 538 (7626):471–476, 2016

[7] Angelos Katharopoulos, Apoorv Vyas, Nikolaos Pappas, and Franc¸ois Fleuret. Transformers are rnns: Fast autoregressive transformers with linear attention. In International conference on machine learning, pages 5156–5165. PMLR, 2020.

[8] Steven Morad, Ryan Kortvelesy, Stephan Liwicki, and Amanda Prorok. Reinforcement learning with fast and forgetful memory. Advances in Neural Information Processing Systems, 36, 2024.

[9] Maximilian Beck, Korbinian Poppel, Markus Spanring, Andreas Auer, Oleksandra Prudnikova, ¨ Michael Kopp, Gunter Klambauer, Johannes Brandstetter, and Sepp Hochreiter. xlstm: Extended long short-term memory. arXiv preprint arXiv:2405.04517, 2024b.

Neurocoder Tales

Discussion about this post