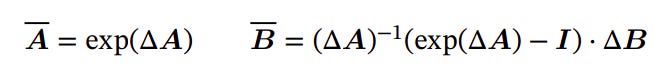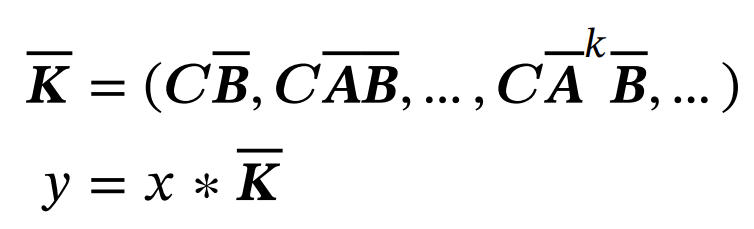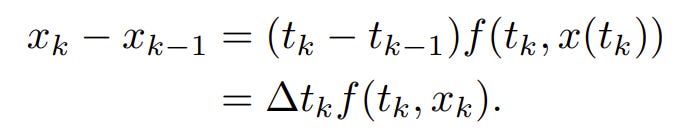The Mamba Effect: State Space Models Taking on Transformers
Mamba: Linear-Time Sequence Modeling with Selective State Spaces (Outstanding Paper Award, COLM 2024)
Table of Content
Large Language Models, Transformers, and the Fundamental Bottleneck
Large Language Models (LLMs) are pretrained on massive datasets to achieve AGI (Artificial General Intelligence). As an unwritten rule, the Transformer [9] architecture is the backbone of LLMs because it can capture rich representations through attention layers. These layers provide direct access to past inputs at any point during processing. However, this capability comes with a computational cost of O(L2) complexity, where L is the number of timesteps (tokens) the Transformer needs to process.

With the development of advanced GPUs and significant investment in AI infrastructure, the quadratic complexity of Transformers has become less of a barrier, allowing Transformer-based LLMs (like OpenAI's ChatGPT, Anthropic's Claude, and Google's Gemini) to achieve excellent results and gain widespread popularity in many real-world applications. However, there are concerns about the Transformer approach:
❌ Transformer intelligence, driven by attention mechanisms, is artificial and doesn't reflect human intelligence. Unlike Transformers, humans cannot access any past input directly. Instead, our brains process information recurrently, compressing past experiences into memory and using the memory to produce outputs—similar to how RNNs (Recurrent Neural Networks) operate.
❌ Reflecting on energy efficiency, recent analyses suggest that the energy expenditure for training current Large Language Models (LLMs) for basic text generation is on par with the energy required to support two individuals in the United States or potentially up to six individuals in countries with lower energy usage. Concurrently, while the human brain boasts a memory capacity in the petabyte range, an LLM with 200 billion parameters equates to 800 gigabytes of storage, constituting approximately 0.08% of the human brain's memory capacity. This implies that achieving human-level memory capacity with LLMs would require significantly larger models, resulting in much higher energy consumption.
❌ Despite the ongoing advancements in Transformer-based large language models, there remains a notable gap compared to human input length capabilities. Even with impressive maximum context lengths, such as 1 million tokens, it only equates to the content of around five novels. In contrast, humans can process and comprehend a far greater volume of information throughout their lives, not to mention the additional input signals we receive from visual, auditory, and other sensory sources.
👀Mounting evidence suggests that existing Transformer models fall short of a fundamental principle necessary to attain genuinely human-like intelligence.
Consequently, recent critiques challenge the efficacy of this approach, advocating for alternative computational frameworks for LLMs, with Mamba [1] emerging as a notable contender.
Mamba Dissection: A Top-Down Approach
🧠 What is Mamba? Mamba is a deep learning architecture that integrates State Space Models with conditional computing, optimized with hardware-aware implementation for fast training. Mamba is built on a series of works centered around State Space Model (SSM) concepts (see Figure below). Each paper can be quite complex. The good news is, we don't need to delve deeply into them to understand Mamba. In this section, I will encapsulate these underlying concepts to explain Mamba, assuming the existence of its building blocks. I aim to make the content straightforward and suitable for those interested in learning only about Mamba. In other blog posts, I will jump into the details of each building block.
Linear-Time Decoding
From a bird's-eye view, Mamba is a computational block or layer that takes one vector as input and returns one vector as output. It functions similarly to a multi-layer perceptron (MLP) layer or a multi-head attention (MHA) layer, transforming input tensors into output tensors. As depicted in the below figure, the Mamba block combines established convolution (Conv, CNN) and MLP layers with a novel Selective SSM block, together with skip connections and common activation functions. One important feature of the Mamba block is that it does not require attention to previous timesteps. All you need for computation is the current timestep input. This translates to a game-changing linear time complexity (O(L)) during inference.
👀 In simpler terms, processing a sequence twice as long takes only twice the time, whereas, for a Transformer, it takes four times as long. Mover, it does not assume a fix-length context window like Transformers.
This isn't a major advantage, as any recurrent network (RNN) can have these properties. The problem with RNNs is their subpar performance compared to Transformers, as they tend to forget quickly due to the vanishing gradient problem. More powerful than RNNs, enhanced Transformers with simplified attention can achieve linear time complexity. Unfortunately, their performance still falls short of the full-attention Transformers.

The question is, 🧠 can Mamba achieve the same high performance as Transformers while maintaining the decoding efficiency of RNNs? According to recent empirical results, the answer appears to be yes [1]. This is already good news. The even better news is that despite its RNN-like structure, the Mamba block can be trained parallelly. We'll delve into that later in the blog, but it's a crucial detail that significantly influences Mamba's design. In simple terms, we now have a new computational block that can be:
✔️ Efficiently trained through parallelization on GPUs
✔️Offers linear-time decoding plus infinite context length like an RNN
✔️Delivers performance comparable to full-attention Transformers.
🧠 Almost too good to be true! But why? It's all thanks to the Selective SSM block. Yes, at the heart of the Mamba block lies the Selective SSM block. This mystical component closely resembles prior SSM architectures used for sequence processing but with a twist. We'll zoom into its secrets later to understand how it empowers the Mamba block.
State Space Model Foundation
A State Space Model (SSM) describes a system using latent (state) variables and differential equations to map a continuous input signal x(t) to output y(t). In the context of Mamba, the SSM has the form:
In this expression, h(t) represents the state variable at a continuous time t, while A, B, and C denote the parameters that define the system's dynamics. Here, A ∈ ℝN×N, B ∈ ℝN , C ∈ ℝN and x,y∈ℝ and h∈ℝN. In practice, the SSM mapping can be independently applied to each dimension when working with vector inputs.
👀 There may be concerns about losing information that captures cross-dimensional relationships when SSM is applied independently to each dimension. However, as illustrated in the figure above, when utilized within the Mamba block, there are additional transformations such as MLP and Conv that blend the dimensional inputs prior to their input to the SSM block.
Note that the SSM is designed for continuous inputs, while LLM inputs are often discrete text. Proper discretization is necessary to preserve SSM properties by using discrete inputs.
Discretization has deep connections to continuous-time systems which can endow them with additional properties such as resolution invariance … and automatically ensuring that the model is properly normalized.
Source: [1]
Many discretization rules can be applied. A common rule used in prior SSM papers is Bi-linear:
Here the authors use the zero-order-hold (ZOH) rule:
where Δ is the discretization step. A bigger Δ results in a sparser representation of the input data, potentially losing some fine-grained details. Conversely, a smaller Δ captures more detailed information, leading to a denser representation.
Using the rule, we have the discrete SSM:
where t now is the timestep. If you're interested in the derivation of the discretization, you can find it at the end of the article. For now, we can encapsulate the SSM computation blocks as:
The computation process is now straightforward and similar to RNN dynamics. In machine learning, we are typically given x in the form of a discrete sequence and must learn A, B, C, and Δ to control the output as desired. This learning process can be achieved through backpropagation as in other deep learning methods.
👀 The learning process in classic SSM is somewhat opposite to what we're doing here. In traditional optimal control, where SSM originated, the system parameters are typically fixed, and we must alter the input to control the state and output as desired.
The advantage of SSM lies in its efficient computation during training. However, if we use the recurrent form, we lose the ability to parallel the computation. Thankfully, SSM theory provides an equivalent representation in convolution form, allowing us to perform parallel convolution computations and maintain the benefits of SSM. To compute SSM using convolution, we first calculate a kernel and then apply an efficient convolution operation (see detailed derivation later):
The kernel K can be stored as a vector of dimension L, where L is the number of timesteps in the input sequence. Once training is complete, K is fixed and only needs to be computed once. However, during training, the parameter matrices change, necessitating multiple computations of K, each naively requiring O(N2L2) operations (not assuming storing cached Āk, which will prevent parallelization).
To efficiently compute the kernel, we can map it to the frequency domain using the z-transform and compute its spectrum instead. Essentially, the sum of a matrix power series in z-transform form corresponds to a matrix inverse. Since mapping between the frequency domain and the time domain can be done efficiently with the (inverse) Fourier Transform, the computational cost becomes O(LN3+LlogL), where N3 represents the cost of a naive matrix inverse. However, the cost can be reduced further as the authors propose using a special kind of matrix A and demonstrate an effective method to invert this matrix using Diagonal Plus Low-Rank reparameterization [2], which results in O((L+N)log(L+N)+LlogL)~O(LlogL) with a big constant factor. In practice, given input sequence data x (batch size B, length L, and dimension D), computing complexity is O(BLDlogL) and can be done in parallel.
An example of such a suitable matrix for A is the HiPPO matrix [4]:
Since we learn A during training, the HiPPO matrix is used to initialize A with the goal of:
Ensuring that the hidden state of the SSM can capture long-term inputs due to the theoretical properties of the HiPPO matrix.
Making A suitable for Diagonal Plus Low-Rank reparameterization, enabling efficient convolution computation.
👀 In Mamba, HiPPO is not recommended. The authors use different diagonal matrix as initialization.
Since we are assuming A has some structures (e.g., diagonal), the corresponding SSMs are referred to as Structured SSMs (S4). Further details on S4 can be found in another blog post. For now, we assume that the convolution view on SSM can be executed efficiently for S4.
Selective State Spaces
Now, let's delve into the new features that Mamba brings to its SSM: adaptive B and C parameters that adjust based on the input data, enabling the parameters to change across timesteps. It's no surprise that a sequence model needs this kind of flexibility, as seen in many well-known works:
The attention mechanisms in Transformers.
The gating mechanisms in Long Short-Term Memory (LSTM, [5]) and Gated Recurrent Units (GRU, [6])
The fast weight mechanisms in HyperNetworks [7] or Stored-Program Memory [8]
These adaptive features enhance the ability to handle varying input data, making it a robust and versatile model for sequence processing. For example, in tasks like Selective Copy and Induction Heads, a standard SSM would struggle because its parameters A, B, and C are fixed after training. These tasks require dynamic computation that varies across timesteps based on the input values.

To handle these tasks, conditional computing needs to be applied to the SSM dynamics. Given that the A matrix is already carefully designed, it makes more sense to adapt B, C, and Δ. Concretely, the authors propose to compute them based on the input data x (batch size B, length L, and dimension D) as follows:
In simple words, neural networks map each item xb,l to different vectors Bb,l, Cb,l , Δb,l used in the SSM dynamics, and thus, the dynamics now is conditioned on the data. After B and C are generated, they will be discretized and used in the SSM computing block.
👀 The authors theoretically show that designing the mapping this way means that the classical gating mechanisms of RNNs are essentially a specific case of their selection mechanism for SSMs. The proof is simple, see at the end.
The authors explain the impact of selectivity mechanisms as follows:
A large Δ resets the state h and focuses on the current input. A small Δ preserves the state h and ignores the current input. Depending on the importance of the input token, Δ can be adjusted to ignore or focus on it.
By making B and C selective, the model gains finer control over integrating input into the state h or propagating the state to the output. This allows the model to modulate recurrent dynamics based on content (input) and context (hidden states).
While the A parameter could also be selective, its effect on the model depends on its interaction with Δ via A=exp(ΔA). Since, Δ is already selective, making A selective may yield no major difference.
👉 Now, here's the dilemma. SSMs can be efficiently implemented using convolution when there's no input-dependent selectivity (time-invariant). But when selectivity is introduced (time-varying), SSMs can no longer be treated as simple convolutions. 🧠 How can we maintain fast training while enhancing SSM with selectivity?
To answer the question, we first need to revisit the computation bottleneck of SSM in the recurrent form:
❌ The main drawback of recurrent computation is the lack of parallelism. Without parallelism, the complexity is O(BLDN), making it much slower than parallel convolution computation, especially when N is large.
❌ Another issue is the large memory usage required to cache the intermediate results.
Mamba tackles these challenges with clever engineering, not complex theory like S4:
✔️ Parallelizing SSM calculations: Mamba leverages algorithms like the Blelloch scan to perform the core SSM computations in parallel, taking advantage of the model's linear dynamics. This significantly speeds up processing.
I will explain the idea conceptually. In the recurrent SSM form, the second equation (multiplying with C) can be easily done in parallel given the ht, and thus, we'll focus on the first equation that defines Mamba state-space dynamics:
Since the second term even with selective SSM only depends on the current timestep (t), we can parallelize its calculation across all timesteps (assuming enough cores). This makes preparing the second term's values constant time (O(1)). Let us denote the second term as bt for short. If we unroll the recurrence, what we want to compute is:
Computing the product of t matrices A can be done using parallel scanning, similar to performing a prefix sum. For example, assuming t=7, we can denote x0=x1=…=x7=A and perform the prefix sum (or product) idea as follows:
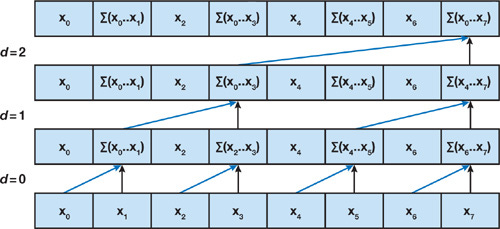
Now we have the final result in the last slot of the memory array (after final transformations like multiplying with h0). The computation time is O(log t), assuming computations in the same computing level d can be run in parallel. The total number of computations remains O(t). We then proceed with the down-sweep phase to retrieve all accumulated values from i=1 to t and store them back in the original array with similar time and operation complexity.
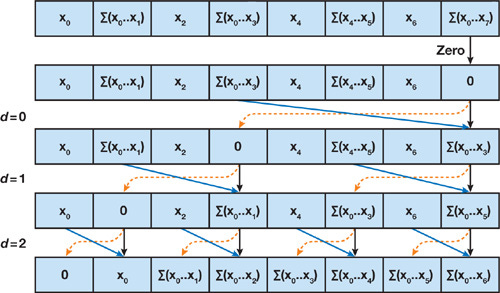
Given the final array x storing Ā for i=0,1,…t, we can shift it right by one, and concurrently multiply each array cell with the array z=[b1,b2,…,bt]. Then, by applying the parallel prefix sum algorithm again, we achieve the array storing all ht. All can be done parallel in O(log t) time. Because of using the scanning algorithm, the authors name the selective SSM as 👉 S6.
✔️ Smart GPU memory allocation: Mamba optimizes how it uses GPU memory, minimizing data movement and reducing both memory footprint and overall running time.
The key idea is to streamline the process by combining the discretization, scan, and multiplication with C into a single kernel:
Load (∆, A, B, C) from slow high-bandwidth memory HBM to fast SRAM.
Discretize A and B in SRAM.
Conduct a parallel associative scan, creating intermediate states of size (B, L, D, N) in SRAM.
Perform multiplication and summation with C, generating outputs of size (B, L, D) and write them back to HBM.
Also, in training, the authors skip storing intermediate states during the forward pass. Instead, these states are recalculated in the backward pass, making the process more efficient. This method is a handy trick to keep memory usage in check during training.
👀 Sounds easy, right? However, it requires a lot of complex CUDA coding (see authors’s code). The final result is that by reducing I/O operations by a factor of O(N), this approach significantly speeds up the process, achieving a 20-40 times improvement in practice.
Mamba Empirical Performance
Now for the exciting part: experiments. Let’s take a look at some of the impressive claims made by the authors:
Mamba achieves 5× higher throughput than Transformers.
It scales linearly with sequence length, handling sequences up to a million in length.
Mamba serves as a general sequence model backbone with state-of-the-art performance in various modalities, including language, audio, and genomics.
In language modeling, the Mamba-3B model outperforms Transformers of the same size and matches the performance of Transformers twice its size in both pretraining and downstream evaluation.
Mamba is Faster than Transformers
This is proven for both training and inference:
Thanks to its optimized implementation, Mamba training is very fast, surpassing even FlashAttention-2 [10], a model already optimized for GPUs, particularly for sequence lengths beyond 2K. Mamba achieves 4-5× higher inference throughput than similarly sized Transformers because it does not require storing attention key-value caches, allowing for larger batch sizes.
In terms of storage efficiency, Mamba is on par with memory-optimized Transformers:
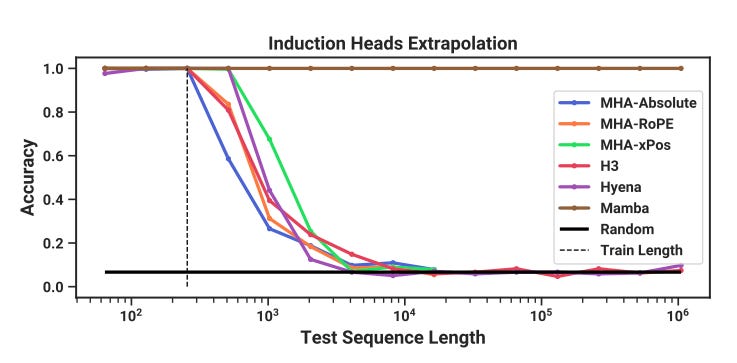
Mamba Scales Linearly up to a Million Tokens
This impressive claim is validated on a simple synthetic task called Induction Heads, which requires selective mechanisms. Despite its simplicity, the task defeats all other baselines except Mamba. Only Mamba maintains perfect accuracy as the sequence length approaches 106.
State-of-the-art Performance
Mamba can achieve SOTA results in certain tasks examined by the authors including DNA modeling and audio generation. For example, on pretraining the Human Genome dataset, Mamba shows better results compared to the SOTA model HyenaDNA.
In the audio generation task, a small Mamba model outshines the state-of-the-art, much larger GAN and diffusion-based models. When scaled up to match the baselines in parameters, Mamba dramatically improves fidelity metrics.
Rivaling Transformers in Language Modeling
On pretraining task using The Pile dataset, Mamba scales more effectively than all other attention-free models and is the first to achieve performance comparable to the best Transformer recipe, which has now become a standard, especially as sequence length increases.
In downstream tasks, Mamba-3B model surpasses Transformers of equivalent size and matches the performance of Transformers with the size of 6-7B.
Ablation Studies
The authors try several configurations of Mamba to prove that the selective mechanism contributes to the performance:
One interesting observation is that A initialization may not need to be strictly theoretical. Simple initialization methods suffice; in certain tasks, we may not necessarily need HiPPO as shown below:
Final Thoughts
🧠 Can Mamba and SSMs challenge Transformers' dominance in the LLM landscape? Possibly. Current results are promising, yet mostly evaluated on synthetic or non-text data. Moreover, with the changes in the S6 layer, Mamba appears not significantly different from other gated RNNs, Linear Transformers or other models with adaptive parameters (they somehow are all linked as shown in a follow-up work [11]), which may compromise its theoretical properties (e.g., linear time-invariant).
Remember that it took several years from the inception of the first Transformer model in 2017 until it became the gold standard in nearly all applications, including LLMs. Therefore, we may anticipate some time before Mamba can truly break through and be adopted by the industry. However, this breakthrough might not happen soon, especially with big tech companies that have already spent a lot of money and are still focused on scaling their LLMs using the Transformer backbone (Chat-GPT 5 is on the horizon).
Appendix
Explanation of the SSM Discretization Formula
Discretization applies to any continuous function x(t) defined by ordinary differential equations (ODEs):
We can compute x as:
This computation may lack a closed-form solution and can be expensive to evaluate for all t. Therefore, it requires discrete-time approximation by integrating over segments of t: [t0,t1],[t1,t2],…,[tk,tk-1], …. The value of xt at each discrete time step can be computed using this formula:
For simplicity, we can rewrite x(tk) as xk and define the step size:
👀 Intuitively, as Δtk converges to 0, we can recover the whole x(t) within [t0,t].
To compute xk, we need to compute the RHS (assuming xk-1 is already computed or known). If f is complex, we must approximate the integral. Simple approximations include:
Euler method: assume f(s, x(s)) ≈ f(tk−1, x(tk−1)) ∀ s∈[tk−1,tk] then:
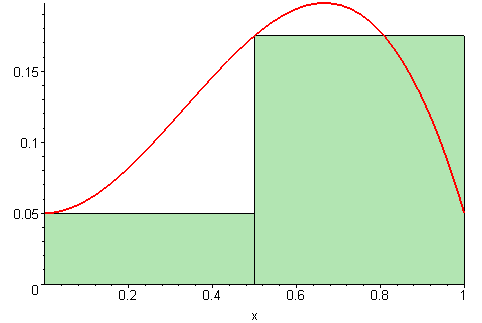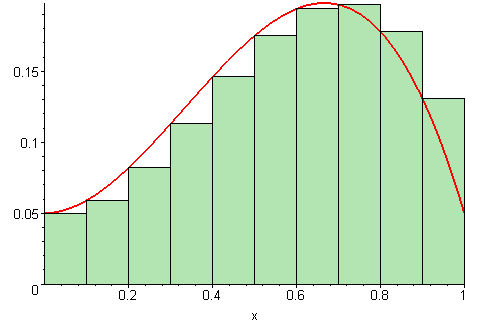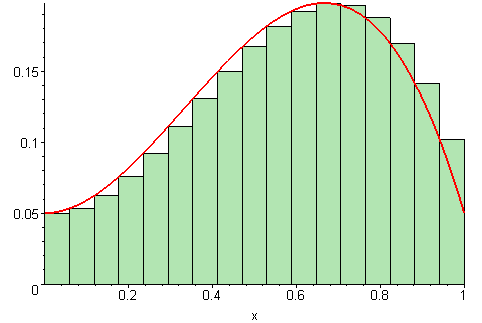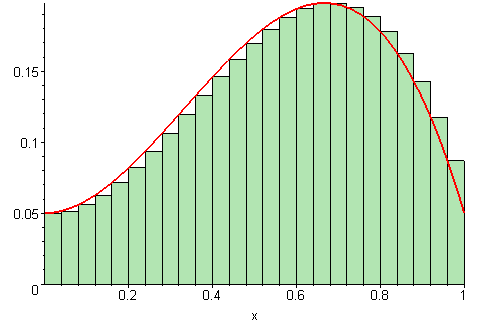
Backward Euler method: assume f(s, x(s)) ≈ f(tk, x(tk)) ∀ s∈[tk−1,tk] then:
Interpolation rule: assume f(s, x(s)) ≈ (1-𝛼)f(tk−1, x(tk−1))+ 𝛼f(tk, x(tk)) ∀ s∈[tk−1,tk] then:

👀 When the parameter 𝛼 is set to 0, the method simplifies to the Euler method. Conversely, when 𝛼 is assigned a value of 1, it transforms into the Backward Euler method.
Returning to the dynamics of the SSM, we have updated the notation to align with the traditional SSM framework for continuous systems. In this context, h is now denoted as x, and x is represented by u. Consequently, we obtain the following SSM dynamics:
Hence,
Plugging this into the equation using the interpolation rule:
Here, uk is like the input data at timestep k and considered constant w.r.t. the hidden state of the SSM. Rearranging 2 sides of the above equation yields:
That is the Bi-linear discretization!
Now comes the more complicated rule that Mamba uses: 👉 zero-order-rule (ZOH). Because SSM is a linear system, the integral can be manageable, and thus, we can solve directly:
To see that, rewrite the original ODE in the case of SSM:
The LHS is actually d(e-Atx(t))/dt. Therefore, taking the integral of both side within the interval [tk-1,tk] yields:
Rearrange 2 sides:
Now is when we use the ZOH assumption which states that u(s) stays the same within the interval (e.g., u(s)=u(tk)), and thus, we have:
We change the variable z=tk-s, then it becomes:
Computing the final integral yields:
That is the ZOH discretization!
SSM CNN-RNN View Equivalence
First, let’s recall what convolution is. At its core, convolution represents a weighted sum, fusing two distinct functions (sequences) to create a new one.

In particular, given the input sequence x=[x1,x2,…,xL] and a kernel K=[w1,w2,…,wL], the convolution formula reads:
In the context of Mamba, the kernel is:
Thus, the convolution view yields:
Remember, if we unfold the RNN dynamics of the SSM:
Given that h0 is initialized to zero and x is a scalar, both perspectives result in the same yt.
Mamba Relation to Gated RNN
First, we review the theoretical result that declares the connection between Mamba and RNN:
In Mamba, Δ=softplus(Linear(xt))=log(1+exp(Linear(xt))), thus applying the discretization rule with the above assumptions yields:
Putting them together, we can prove the theory:
References
[1] Gu, Albert, and Tri Dao. "Mamba: Linear-time sequence modeling with selective state spaces." arXiv preprint arXiv:2312.00752 (2023).
[2] Albert Gu, Karan Goel, and Christopher Ré. “Efficiently Modeling Long Sequences with Structured State Spaces”. In: The International Conference on Learning Representations (ICLR). 2022.
[3] Albert Gu, Isys Johnson, Karan Goel, Khaled Saab, Tri Dao, Atri Rudra, and Christopher Ré. “Combining Recurrent, Convolutional, and Continuous-time Models with the Linear State Space Layer”. In: Advances in Neural Information Processing Systems (NeurIPS). 2021.
[4] Albert Gu, Tri Dao, Stefano Ermon, Atri Rudra, and Christopher Ré. “HIPPO: Recurrent Memory with Optimal Polynomial Projections”. In: Advances in Neural Information Processing Systems (NeurIPS). 2020.
[5] Hochreiter, Sepp, and Jürgen Schmidhuber. "Long short-term memory." Neural computation 9, no. 8 (1997): 1735-1780.
[6] Cho, Kyunghyun, Bart Van Merriënboer, Caglar Gulcehre, Dzmitry Bahdanau, Fethi Bougares, Holger Schwenk, and Yoshua Bengio. "Learning phrase representations using RNN encoder-decoder for statistical machine translation." arXiv preprint arXiv:1406.1078 (2014).
[7] Ha, David, Andrew Dai, and Quoc V. Le. "Hypernetworks." arXiv preprint arXiv:1609.09106 (2016).
[8] Le, Hung, Truyen Tran, and Svetha Venkatesh. "Neural stored-program memory." arXiv preprint arXiv:1906.08862 (2019).
[9] Vaswani, Ashish, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Łukasz Kaiser, and Illia Polosukhin. "Attention is all you need." Advances in neural information processing systems 30 (2017).
[10] Dao, Tri, Dan Fu, Stefano Ermon, Atri Rudra, and Christopher Ré. "Flashattention: Fast and memory-efficient exact attention with io-awareness." Advances in Neural Information Processing Systems 35 (2022): 16344-16359.
[11] Dao, Tri, and Albert Gu. "Transformers are SSMs: Generalized models and efficient algorithms through structured state-space duality." arXiv preprint arXiv:2405.21060 (2024).