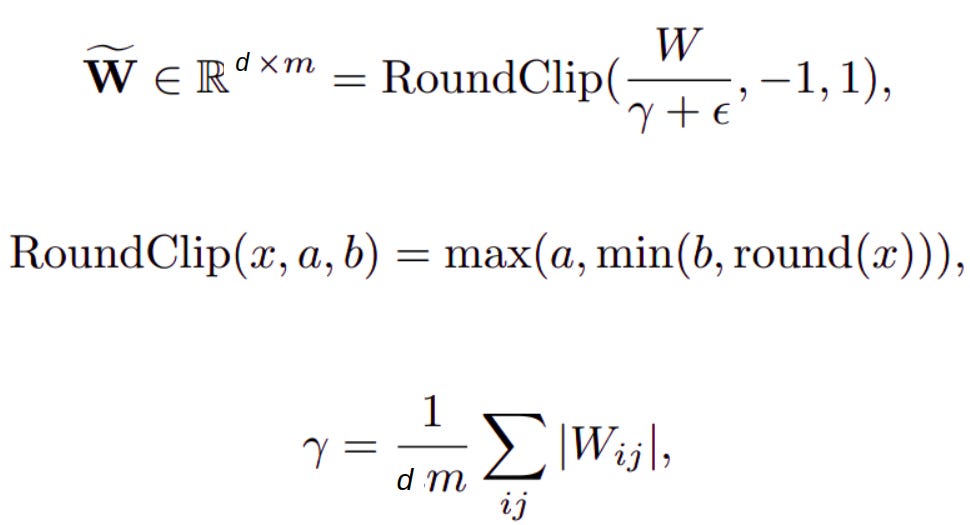Cheap Large Language Models via Eliminating Matrix Multiplications
Scalable MatMul-free Language Modeling
Table of Content
Why Large Language Models are Expensive?
Large Language Models (LLMs) have many layers. For instance, the largest GPT-3 model, with 175 billion parameters, utilizes 96 attention layers, each containing 96 heads with 128 dimensions. Since each attention layer is coupled with several feed-forward layers, all of which heavily rely on matrix multiplication (MatMul) operations, we can say that MatMul dominates their overall computational cost.
To recap what is MatMul, see the example below:

Typically, each cell in the RHS requires d multiplication and d-1 additions. Thus, computing the product of two d×d matrices requires d3 multiplications and d3 -d2 additions, resulting in O(d3) floating-point operations. A similar MatMul operation can be applied to Matrix-Vector multiplication, a special case of Matrix-Matrix multiplication.
The good news is that we can perform parallel computations using GPUs. With sufficient cores, the time complexity can be significantly reduced. For instance, using O(d3) cores with a naive matrix multiplication approach can achieve an O(logd) time complexity in an ideal scenario with no communication or I/O overhead. (Refer to my previous post for related information).
👀 In practice, people often use a divide-and-conquer approach to implement MatMul in parallel. Especially, one can use Strassen algorithm with less than O(d3) multiplications (~O(d2.8)). This class of algorithm usually has parallel time complexity of O(log2d). See explanation at the end.
Unfortunately, parallel computing comes with its own set of challenges:
❌ GPU is expensive.
❌ While it can reduce the computation time, it does not decrease the total amount of floating-point operations required while sometimes even increasing them.
Consequently, the number of operations remains approximately O(d3) and we have to employ big GPUs to make the computation fast. This costs more money. Given the huge amount of operations, it will take hundreds of years to train LLMs using a single GPU. Depending on the size of the LLMs, the training time, and the amount of training data, the actual costs can vary [1]. However, as a general rule of thumb, pretraining a model with billions of parameters can cost millions of US dollars.

Memory usage is another significant cost factor. For instance, without quantization, as each parameter needs 4 bytes to store, a model with 175 billion parameters requires 700 GB of memory. Consequently, handling such a model would necessitate dozens of V100 GPUs, further driving up the cost.
These challenges highlight the need for new solutions that can:
✔️ Reduce the number of floating-point operations
✔️ Decrease the memory required for storing the results
👉 Improving matrix multiplication (MatMul), a dominant operation that consumes most of the computational resources and memory, is crucial. 🧠 The question is whether we can eliminate MatMul without compromising the performance of LLMs. The paper Scalable MatMul-free Language Modeling [7] comes with a potential yes answer.
Background: BitLinear Layer
The fundamental layer of neural networks is the Linear Layer (or Feed-forward Layer), which performs a matrix multiplication to map the input x∈ℝd to the output y∈ℝm using the weight matrix W∈ℝd×m. For i=1,2,..m:
Here, for each dimension of the output y, we need to take d multiplications and d-1 additions. With a special weight matrix such as 👉 ternary weight matrix where each parameter can be either {-1,0,1}, the MatMul becomes:
Here, we can see that thanks to the ternary weights, for each dimension of output, we only need to perform at most d-1 additions and subtractions, which reduces the multiplication cost compared to normal MatMul.
👀 The paper also use ⊛ to represent a ternary MatMul. The Linear Layer using ternary MatMul becomes BitLinear layer, which is introduced in prior work [2].
Using BitLinear can result in some computational overheads:
Weight quantization, converting a normal weight to a ternary weight:
Activation quantization, reducing x to 8-bit precision
where ϵ is used to avoid overflow during clipping. These overheads are small compared to multiplication in MatMul. For example, weight quantization is typically performed infrequently, only after the weights are updated.
👀 More importantly, quantization automatically reduces the size of the model weights, thus lifting memory cost burden.
Another important trick is to ensure numerical stability post-quantization, achieved by applying RMSNorm [3] before quantizing activation:
Here, output re-scaling is necessary because, during weight and activation quantization, the inputs and weights have been multiplied or divided by β, γ and Qb.
Like the Mamba paper, this paper emphasizes GPU-efficient implementation and introduces hardware acceleration. As the paper points out, naive implementation involves multiple I/O operations: reading activations into SRAM for RMSNorm, writing back for quantization, and further processing. Thus, to streamline efficiency, operations are fused, reading activations only once for RMSNorm and quantization directly in SRAM.
With the background on BitLinear equipped, we are now ready to explore the paper's primary contribution: the design of a MatMul-free large language model (LLM).
MatMul-free Architectures
Before we begin, let’s clarify the naming preference:
Channel-mixer: a module that transforms an input vector into output by utilizing all features (spatial information) across all dimensions of the input and mixing them to produce the output. Examples include MLPs or Gated Linear Units (GLUs).
Token mixer: a module that transforms sequences of input tokens into outputs. In classic LLMs, this is typically achieved through the Self-Attention mechanism, while in Mamba, it involves the Selective SSM. The module needs to capture temporal relationships between timesteps to infer the appropriate output at each timestep.
MatMul-free Channel Mixer
BitLinear layer can be simply applied to any Channel Mixer architecture to make it MatMul-free. In this case, it applies to GLU, resulting in a new layer defined by a series of computations:
👀 Here, l, often greater than d, represents the dimension upscaling technique. Similar to Llama, the paper keeps GLU with a total parameter count of 8d² by setting the upscaling factor to 8/3d.
MatMul-free Token Mixer
The authors have tried several well-known Token Mixer architectures with the BitLinear techniques to make them MatMul-free. Below are the insights:
❌ Self-Attention: Fail!
The authors quantize Q and K with ternary values to eliminate MatMul in the self-attention operation, but the model trained this way fails to converge. They hypothesize that crucial outlier values in activation are ignored during Matrix-Matrix MatMul quantization. To address this, they avoid quantizing Matrix-Matrix multiplication components 👉 switch to ternary RNNs.
✔️ Gated Recurrent Unit (GRU [4]): Work!
GRU only involves matrix-vector multiplication, making it safe for quantization. Its gating mechanism is also beneficial for capturing essential information over long sequences. However, one potential issue is recurrence is slow to compute. Hence, the authors propose to adopt recent techniques to speed up RNN.
👀 Here, the techniques are actually not new: simplifying the architecture by using linear operations and avoiding non-linear activations (tanh) between the hidden state dynamics (even only using diagonal hidden state weight matrix!). Linear dynamics allows parallelization while being able to capture long-term dependencies , as explained in the Mamba blog.
The final architecture, called 👉 MLGRU, looks like:
Although non-linear activations (σ) are present, they do not affect the recurrence dynamics (red box) and can be computed in parallel.
✔️ Recurrent Weighted Key Value [5] (RWKV-4): Work!
Similarly, all recurrence dynamics (red boxes) here are linear, allowing for parallel computation (O(log L)) with L being the number of time steps. Unlike MLGRU, RWKV-4 introduces less hardware-efficient exponential and division operations, so MLGRU is preferred.
Important Training Tricks
Given the numerous quantization steps and the sparse (ternary) nature of the networks, careful consideration of the training procedures is necessary:
Straight-Through Estimator. The authors use the straight-through estimator (STE) [6] as a surrogate function for the gradient in quantization steps, particularly for Clip and Sign functions. 🧠 How does it work? In forward pass, the actual non-differentiable function (e.g., clipped values) is used to compute the output. In the backward pass, a surrogate gradient, which is a differentiable approximation of the original function’s gradient, is used instead of the true gradient.
Larger Learning Rate. When training language models with ternary weights, using standard learning rates can lead to insignificant updates that don't affect clipping. This hinders effective weight updates, causing biased gradients. To overcome this, higher learning rates (order of 10-3) are often used for binary or ternary weight models to promote faster convergence.
Special Learning Rate Scheduler. In particular, they utilize a cosine learning rate scheduler and halve the learning rate midway through training.
Empirical Performance
When assessing computational costs, a useful benchmark is testing the scaling law, which evaluates training performance (loss) relative to computational cost (FLOPs). In the paper, various sizes of LLMs are trained on the SlimPajama dataset, demonstrating the following results:

👀 While the initial results are promising, larger-scale testing is necessary to validate the scaling law of MatMul-Free LLMs.
In terms of memory and speed, MatMul-Free LLMs (MLGRU) win over Transformer-based LLMs:
This result is not surprising because MLGRU uses ternary weights and MatMul-free parallel computation, hence reducing memory and computing costs, respectively.
Final Thoughts
It's fascinating to witness the resurgence of RNNs in comparison to Transformers. Just a few years ago, empirical evidence suggested that RNNs couldn't scale effectively and significantly underperformed Transformers and other attention-based architectures in key domains. However, it now appears that RNNs struggled primarily because we hadn't yet found efficient ways to scale them up. As the number of parameters reaches into the billions, RNN-like architectures are demonstrating competitive performance, as evidenced in this paper and the Mamba paper.
The key idea lies in parallelizing RNN training, which has become increasingly feasible with modern techniques. 👉 One crucial principle for achieving this is maintaining linear recurrent dynamics (an old idea [8] but recently scaled up). Although this approach sacrifices some representational capacity, it can be offset by incorporating non-linear transformations in other parts of the network that do not impede parallelization. This compensation has proven sufficient to deliver strong performance while enabling faster training and inference, and reducing memory usage compared to Transformers.
Appendix
Time Complexity of Parallel Matrix Multiplication
There are various methods to compute MatMul in parallel. A common approach is using a divide-and-conquer strategy, which maintains a reasonable number of computing cores while achieving fewer total operations and faster speedup. In this section, I will intuitively explain the approach and its time complexity utilizing parallel cores.
The approach assumes that the matrix dimensions are powers of 2. This assumption can be easily relaxed, e.g., by padding the matrix with zeros to fit the required size. It uses the block partition property of matrix multiplication:
This formulation breaks down an n×n matrix multiplication into 8 multiplications (MULT) and 4 additions (ADD) of n/2×n/2 submatrices, which can be executed recursively.
Let's start with ADD. The algorithm also divides the matrix into 4 submatrices and recursively calls the addition function with the smaller submatrices as inputs. For example, to sum matrix C and T of size n, the function call looks like:
Assuming we can call the 4 inner ADD functions in parallel, then the waiting time is only the processing time of one inner ADD plus some constant (w.r.t n) overhead computation to allocate variable storage. Concretely, let us denote A the time function needed for the function call ADD at size n, then we have:
👀A more precise notation would use Θ instead of O. However, I use O here for simplicity.
To solve this recursive equation, we can use the Master Theorem. I won't delve into the theorem's form and proof here, but intuitively, we expect the solution to be in the form of A(n) = O(logn) because when we equate both sides:
Next, let's analyze the MULT function, which involves 8 multiplications of submatrices followed by summing up the results. A simplified representation of the MULT function, multiplying matrices A and B to store the result in matrix C of size n, would look like:
Here, T is a temporary result matrix, and we can execute all 8 inner MULT operations in parallel. However, we must wait for all of them to finish before calling the final ADD function, and finally, we must wait for the ADD function to finish. Therefore, the time function M needed for the function call MULT at size n is:
Again, we can use the Master Theorem to solve this equation, and the result is M(n)=O(log2n). To roughly verify, just assume M(n)=alog2n for all a, and substitute the solution to see that:
which is equivalent to a fact:
So, the parallel time complexity of MatMul is O(log2n) and the approach only uses a fixed number of cores. For more details, see this.
References
[1] https://medium.com/@dzmitrybahdanau/the-flops-calculus-of-language-model-training-3b19c1f025e4
[2] Wang, Hongyu, Shuming Ma, Li Dong, Shaohan Huang, Huaijie Wang, Lingxiao Ma, Fan Yang, Ruiping Wang, Yi Wu, and Furu Wei. "Bitnet: Scaling 1-bit transformers for large language models." arXiv preprint arXiv:2310.11453 (2023).
[3] Zhang, Biao, and Rico Sennrich. "Root mean square layer normalization." Advances in Neural Information Processing Systems 32 (2019).
[4] Cho, Kyunghyun, Bart Van Merriënboer, Caglar Gulcehre, Dzmitry Bahdanau, Fethi Bougares, Holger Schwenk, and Yoshua Bengio. "Learning phrase representations using RNN encoder-decoder for statistical machine translation." arXiv preprint arXiv:1406.1078 (2014).
[5] Peng, Bo, Eric Alcaide, Quentin Gregory Anthony, Alon Albalak, Samuel Arcadinho, Stella Biderman, Huanqi Cao et al. "RWKV: Reinventing RNNs for the Transformer Era." In The 2023 Conference on Empirical Methods in Natural Language Processing.
[6] Yoshua Bengio, Nicholas Léonard, and Aaron C. Courville. Estimating or propagating gradients through stochastic neurons for conditional computation. CoRR, abs/1308.3432, 2013.
[7] Zhu, Rui-Jie, Yu Zhang, Ethan Sifferman, Tyler Sheaves, Yiqiao Wang, Dustin Richmond, Peng Zhou, and Jason K. Eshraghian. "Scalable MatMul-free Language Modeling." arXiv preprint arXiv:2406.02528 (2024).
[8] Arjovsky, Martin, Amar Shah, and Yoshua Bengio. "Unitary evolution recurrent neural networks." In International conference on machine learning, pp. 1120-1128. PMLR, 2016.