Extending Neural Networks to New Lengths: Enhancing Symbol Processing and Generalization

Plug, Play, and Generalize: Length Extrapolation with Pointer-Augmented Neural Memory

Oct 23, 2024

PANM: Pointer-augmented Neural Memory Architecture. Source.

Introduction to the Length Extrapolation Problem

Length extrapolation in ML/AI refers to the ability of a model to predict outputs for sequences that are significantly longer (or shorter) than those it was trained on. This is a common challenge AI models face, particularly in tasks involving sequential data like natural language processing or time series analysis.

Many deep sequence learning models struggle to generalize to longer or more complex sequences than those encountered during training. In other words, they perform well on sequences of similar length to the training data but fail catastrophically when predicting longer sequences. This "extrapolation" problem remains one of the few unresolved challenges in modern AI.

The Machine Learning Guide for Predictive Accuracy: Interpolation and Extrapolation | by Ryota Kiuchi, Ph.D. | Towards Data Science — Interpolation (left): testing data lies within training data (same length). Extrapolation (right): testing data is outside training data (different length), Source.

For example, while modern sequence models like Transformers and LSTMs are powerful, they often fail to:

Extrapolate to longer sequences (e.g., if trained on sequences of length 10, they fail on sequences of length 20+).
Generalize in symbolic tasks, such as copying, sorting, or arithmetic, which require capturing the true symbolic rules to guarantee testing performance.

👀 The issue also affects big models like Large Language Models, making them struggle with symbolic manipulation tasks. 👉 Current methods lack a principled mechanism for systematic generalization

PANM, or Pointer-Augmented Neural Memory [5], introduces a novel approach to solving this challenge by emulating symbolic processing through memory pointers—a concept inspired by computer architecture and programming. PANM’s explicit pointers act like computer memory addresses, enabling better symbol manipulation and length extrapolation.

This blog dives into how PANM works, explains its design with simple mathematics, and highlights its performance across key NLP tasks.

Why Do Neural Networks Struggle with Length-Extraploation?

Neural networks are typically trained on a dataset with a specific distribution of sequence lengths. If the test data contains sequences that are significantly different in length from the training data, the model may struggle to generalize.

Take RNN as an example (Transformer and other sequence models have similar issues), 👉 the root cause lies in the way hidden states accumulate information over time. As longer sequences are introduced during testing, the range of accumulated values can differ significantly from those experienced during training, leading to distribution shifts and poor predictions.

The general RNN update equation (without nonlinearity activation for simplicity) is:

\(h_t = W h_{t-1} + U x_t + b \)

We can express the hidden state at time T by unrolling the recurrence relation over all previous steps:

\(h_T = W^T h_0 + \sum_{t=1}^{T} W^{T - t} (U x_t + b) \)

Here, h_T depends on both the initial state h₀ and the accumulated inputs from all previous time steps. The sum grows as the sequence length increases, making the model sensitive to the number of steps processed. During training, the model sees sequences of length T_train. Even in the simplest case where W=1, if we assume the input x_t at each step is drawn from a normal distribution x_t∼N(0,σ²), the sum of inputs overall steps will have a variance proportional to the length of the sequence:

\(\text{Var}\left(\sum_{t=1}^{T_{\text{train}}} U x_t\right) = T_{\text{train}} \cdot \sigma^2 \|U\|^2 \)

The problem arises when the RNN is tested on sequences much longer than those seen during training. For a sequence of length T_test, the variance of the accumulated input becomes:

\(\text{Var}\left(\sum_{t=1}^{T_{\text{test}}} U x_t\right) = T_{\text{test}} \cdot \sigma^2 \|U\|^2 \)

If T_test≫T_train, the variance grows proportionally, leading to a distribution shift. Specifically:

\(T_{\text{test}} \gg T_{\text{train}} \implies \text{Var}_{\text{test}} \gg \text{Var}_{\text{train}} \)

As a result, the RNN's learned patterns from the training set may not apply to the test set.

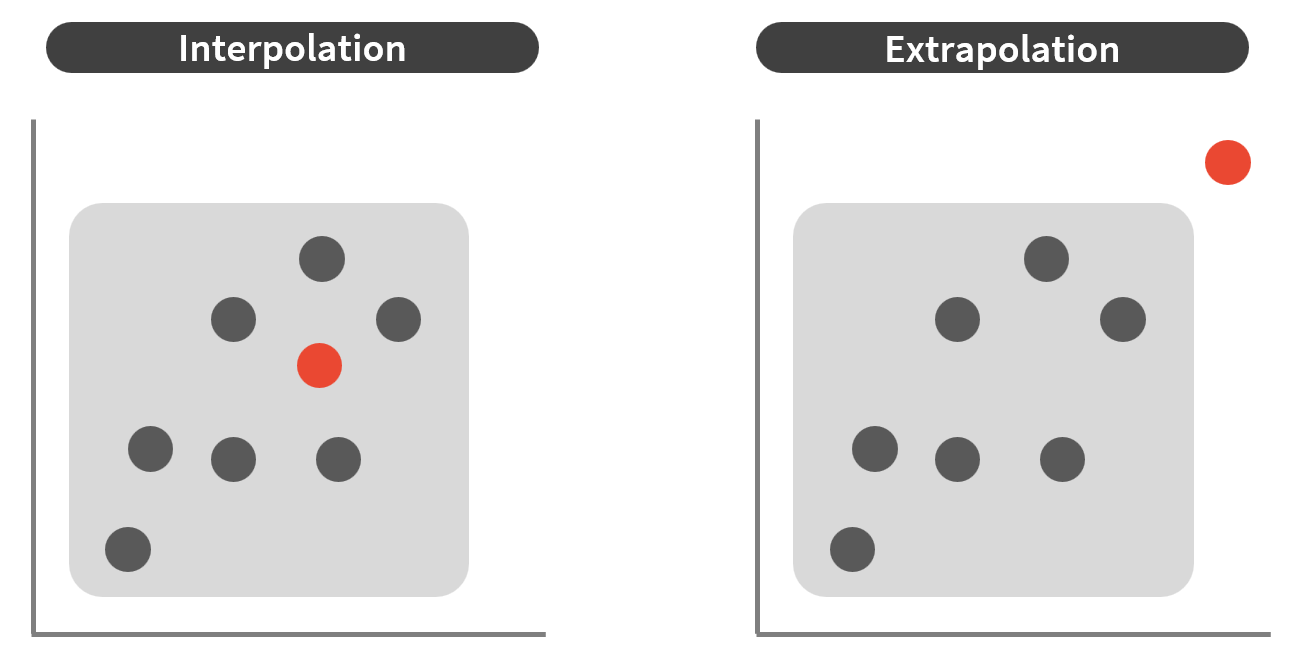
In practice, big training data is often required to handle extrapolation effectively. The idea is to ensure that the training data covers the entire support space, reducing the problem to interpolation during testing. However, collecting and processing such extensive datasets can be costly and impractical.

An alternative strategy is to guide neural networks to learn the underlying rules that govern the data. When the model captures these rules, it can generalize to sequences of any length—even those far beyond what it encountered during training.

This approach is analogous to a programmer who understands the logic behind a task and writes an algorithm capable of solving the problem for arbitrary input sizes. Similarly, a network that learns the intrinsic patterns in the data can extrapolate effectively, just as an algorithm remains valid regardless of the input size.

For example, Copy task is a simple problem used to test whether a model can generalize beyond what it has seen during training. Given an input sequence {x₁,x₂,…,x_T}, the goal is to produce the same sequence as output, {x₁,x₂,…,x_T}. The task can be solved perfectly with a simple Python program:

function COPY_SEQUENCE(input_sequence):
    output_sequence = []  # Initialize empty output

    for i = 1 to length(input_sequence):
        # Copy elements one-by-one
        output_sequence.append(input_sequence[i])  

    return output_sequence

While the task seems trivial, many neural networks struggle to handle sequences much longer than those seen during training, often failing to generalize correctly. They fail to capture the above program, and their performance drops significantly as reported below:

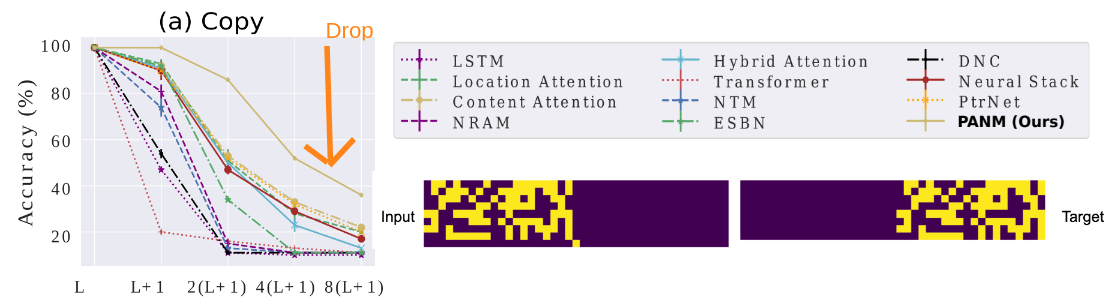
Copy task: Neural networks fail to generalize on longer testing sequence lengths. Source.

👀In contrast to neural networks, neuro-symbolic architectures are well-designed to do length extrapolation [1]. However, neuro-symbolic models are not trained end-to-end, assuming complicated training signals and discrete optimization techniques such as reinforcement learning. They are often task-specific. 🧠 Can we design an alternative method that can genralize while being differentiable, easy to train and making minmal assumptions on the task?

Core Idea: Modeling Pointers to Learn the Symbolic Rules

Design Principles

PANM proposes a pointer-based mechanism built on two key principles:

Explicit Pointers as Physical Addresses:
Instead of relying on softmax-based attention to represent memory locations [2], PANM pointers are designed to act as incremental binary addresses, like physical memory in classical computing. This structure ensures that each memory location is predictable and scalable, critical for handling longer sequences.
Decoupling Pointer Manipulation from Input Data:
In PANM, pointer operations are isolated from the content being processed. This separation allows the model to focus on abstract rules—like copying or sorting—without being influenced by the specific data values.

These principles can be realized as a slot-based RAM inspired by the Von Neumann architecture [3]. Each memory slot contains data and its corresponding address, ensuring the model can reliably store and retrieve information regardless of sequence length.

The key distinction between PANM’s pointers and softmax “pointers“ seen in Pointer Network and Transormer-like architecture is that the PANM pointer is modeled explicitly as a binary number, not a softmax distribution, which will allow a new capability of pointer manipulation.

How Explicit Pointers Power Memory Manipulation and Generalization

Pointers are crucial in computing as they store the memory address of data, enabling efficient data access and manipulation. In C, a pointer p associated with a value d is written as p = &d, where & returns d's address. To access the data at p, we use *p, known as pointer dereferencing.

This flexibility allows for efficient operations. For instance, copying a list X to Y using pointers involves:

Initialization: Set pointers to the first elements of both lists: pX = &X and pY = &Y.
Dereference and Copy: Copy the value at pX to the location pointed by pY: *pY = *pX.
Move Pointers: Increment both pointers to move to the next elements: pX = pX + 1 and pY = pY + 1.

Repeat this process until all elements from X are copied to Y, regardless of list length. In C, the copy program using pointers will look like below:

void copy(int X[], int Y[], int n) {
    int *pX = X;
    int *pY = Y;

    for (int i = 0; i < n; i++) {
        *pY = *pX;
        pX++;
        pY++;
    }
}

Modeling Explicit Pointers in Neural Networks

First, the paper models memory addresses using an address bank A. This bank acts like a range of addresses starting from a base address a_Band increasing sequentially. For example, if a_B= 3 and the address bank contains 3 addresses, we get A = {3, 4, 5}. Each address is represented as a binary vector, so if the address space uses 4 bits, these addresses would be A = {0010, 0011, 0100}.

Given a memory M containing len(M) slots (where each slot holds part of the input sequence), we can map each slot to an address in the bank. The mapping is:

A[t] = &M[t], ∗A[t] = M[t] (1 ≤ t ≤ len(M))

Here, A[t] provides the address of the memory slot, and ∗A[t] retrieves the data stored in it. For generalization, the address space must cover more addresses than the longest input sequence (i.e., 2ᵇ>max(len(X))).

👀 Training with Random Address Sampling During training, the model must see all possible addresses. Otherwise, unexposed addresses could confuse the model during testing. To prevent this, the paper authors randomly sample the base address a_B for each input sequence. This ensures the model learns to handle different ranges of addresses and can generalize to unseen sequences.

Using the address bank, the copy task follows three key pointer operations:

Assignment: Set the pointer for timestep t: p_t = A[t]
Dereference: Retrieve the value at the pointer location: y_t = ∗p_t
Arithmetic: Move the pointer to the next slot: p_t = p_t + 1

This pointer-based approach ensures that the model can generalize to any sequence length, as it follows the same logic regardless of how long the input is. This simple yet powerful technique allows the network to operate like an algorithm, handling unseen scenarios without needing to memorize specific patterns. To learn more about how these concepts make PANM’s pointers differ from previous implicit "pointers," check the details at the end of this post.

Understanding Pointer-Augmented Neural Memory (PANM)

The Pointer-Augmented Neural Memory (PANM) is a novel external memory module designed to implement the aforementioned principles and ideas. Interestingly, PANM can be used in a plug-and-play manner and can be combined with any sequence model to empower the backbone model with explicit pointer manipulation capabilities.

At its core, PANM interacts with a Controller neural network (e.g., an LSTM or Transformer, or even LLMs) to read from and write to memory. These layers can be stacked on top of other sequence models, as depicted below:

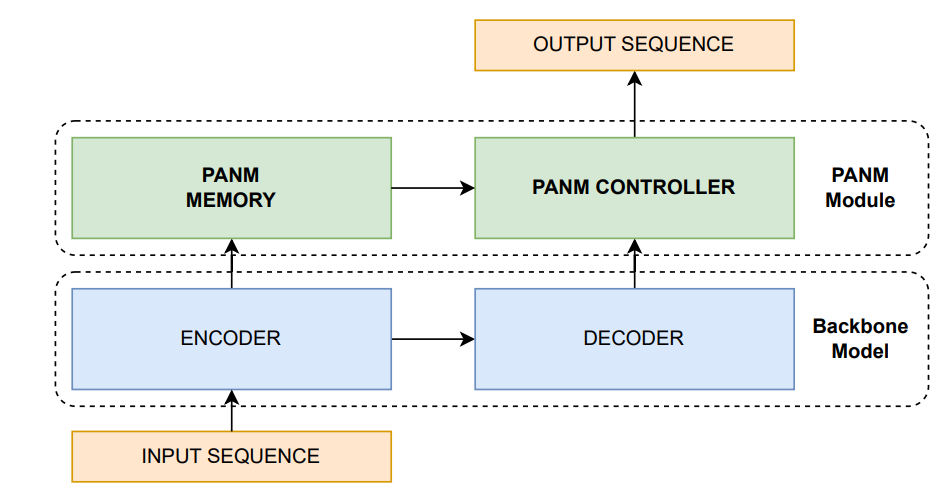
PANM as a plug-and-play architecture. Source.

Unlike traditional neural memories, PANM Memory introduces:

An address bank (A)—a collection of binary memory addresses.
A Pointer Unit (PU)—a module that manipulates pointers to access memory efficiently.

During the encoding phase, the input sequence X is transformed into memory M using an encoder:

\(M = \text{Encoder}_{\theta}(X) \)

The address bank A stores binary addresses, which correspond to the memory slots in M. These addresses serve as pointers, enabling the network to perform flexible and scalable data retrieval, crucial for generalizing to unseen sequence lengths.

Pointer Unit Operations

The Pointer Unit (PU), implemented as a GRU, manages the pointer variables over time. At each decoding step t, the PU updates the pointer based on the previous timestep. The process can be broken down into 3 steps:

Pointer Update: The PU generates a new hidden state using the GRU:

\(h_t^a = \text{GRU}_{\phi}(p_{t-1}^a, h_{t-1}^a) \)

The update represents pointer manipulation or learning the symbolic rules of moving pointers around the memory.

Address Attention: The pointer then interacts with the address bank through attention mechanisms:

\(w_t^a[n] = \text{softmax} \left( \frac{h_t^a \cdot g_\phi(A[n])}{\|h_t^a\| \|g_\phi(A[n])\|} \right) \)

This computes attention weights over all addresses, where g_ϕ is a neural network that maps addresses to the same space as the hidden state.

Pointer Assignment: The final pointer value at step t is computed as a weighted sum of the addresses:

\(p_t^a = A w_t^a \)

This soft assignment ensures the pointer can address any memory slot, even in longer sequences. For example, if the GRU learns to increment the pointers, we can iterate through the data sequence perfectly, regardless of the sequence length. The incremental rule can be learned for any sequence length thanks to the 👉 Base Address Sampling mechanism.

Let’s walk through an example to see how base address sampling improves generalization. Suppose the training sequence length is 10, and the task is to increment a pointer following the rule p′=p+1 (as in a copy task). The address range is {0, 1, …, 19}, which is larger than any sequence length.

If the base address a_B is set to 0, the training address bank becomes {0, 1, …, 9}. Without base address sampling, the model always encounters this same range during training. As a result, it only learns how to increment pointers for 0≤p≤9. If the test sequence requires addresses beyond 9, the model will fail to generalize.

With base address sampling, the base address changes during training. For example, at some point, the base address might be a_B=10, shifting the address bank to {10, 11, …, 19}. Now the model encounters larger addresses and learns the rule p′=p+1 for p>9, such as transforming p=10 to p′=11. This happens because the pointer's value (∗p) is used to predict the output sequence, and the task loss ensures the model learns to apply the correct transformation by updating the Pointer Unit.

At test time, with an input sequence of length 12, the base address is reset to a_B=0. The address bank becomes {0, 1, …, 11}, and the model can still correctly apply the learned rule to new addresses, like p=10→p′=11.

🧠 Is base address sampling efficient? Does it require a large number of training samples to ensure sufficient coverage of base addresses? Check the details at the end of this post!

Two Modes of Memory Access

Given a pointer or its address attention weight, PANM supports two modes for accessing the memory:

Mode 1 (Direct Access): The pointer retrieves data directly from memory, similar to accessing a row in a table.

\(\ast p_t^a = M w_t^a \)

This enables instant access to the pointer's value, which is suitable for memory access after positional manipulations.

Mode 2 (Relational Access): The pointer identifies data based on relationships, such as finding relevant information by comparing entries. This mode allows the network to perform more complex reasoning, like selecting the most important sentence in a document:

Here, the Mode 1 pointer values are used to retrieve other related memory contents through an attention mechanism, identifying entries similar to the ones accessed by the Mode 1 pointer. The pointers and values of these related contents are referred to as the Mode 2 pointer and pointer value.

👀 In Mode 2, the pointer doesn’t just move through memory linearly but retrieves the most relevant information based on similarity between queries and memory addresses. This allows the model to perform tasks requiring reasoning over the content stored in memory, such as summarizing, answering questions, or selecting key events in a sequence.

Relational access enables the model to generalize to unseen data, leveraging learned relationships rather than fixed positions in memory. This flexibility is essential for tasks involving variable-length sequences or complex dependencies between elements.

The Controller: Integrating Mode 1 and Mode 2 Access

The Controller (Ctrl) in PANM decodes memory and produces outputs. Unlike traditional approaches, the Controller utilizes pointer-based memory access to leverage symbolic information from memory. At each decoding step t, the Controller combines the pointer values (from Mode 1 and Mode 2) with an optional decoding input z_t and uses a GRU to generate the hidden state.

At time t, the GRU recurrently updates the hidden state:

\(h_t^c = \text{GRU}_{\lambda} \left( \{\ast p_t^a, h \}_{h=1}^{H_a}, \quad \{\ast p_t^c, h \}_{h=1}^{H_c}, \quad z_t, \quad h_{t-1}^c \right)\)

The initial hidden state at step 0 is computed by summing the memory contents:

\(h_0^c = \sum_{i} M[i] \)

This design allows the GRU to recurrently integrate pointer-based memory access into the content-based input, helping the model maintain a rich hidden state throughout decoding.

The Controller combines the hidden state with the pointer values from both modes to generate the output token. This combination ensures that the model can correctly decode sequences, even when the memory content differs from what was seen during training (e.g., due to longer sequences). The output is produced using a multi-layer perceptron (MLP) g_o, defined as:

\(\hat{y}_t \sim p_\Phi(y_t | X_i, z_t) = g_o \left( \{\ast p_t^a, h \}_{h=1}^{H_a}, \quad \{\ast p_t^c, h \}_{h=1}^{H_c}, \quad h_t^c \right)\)

Notable Empirical Results

Pointers are particularly useful for tasks that demand strong symbol processing abilities. These include simple algorithmic tasks like Copy or Recall. While these tasks may seem straightforward, even advanced models like ChatGPT can occasionally struggle with them.

To generalize on these tasks, models must learn the underlying symbolic rules. For example, in Copy and Sorting tasks, PANM's pointer manipulation corresponds to mode 1 access and mode 2 access, respectively.

Copy and ID Sort: Pointers in actions. In the copy task, only Mode 1 access is required. As the decoding step t progresses, the Pointer Unit generates *pᵃ_t* by incrementing addresses sequentially as expected. In the ID sort task, both Mode 1 and Mode 2 are needed. The Pointer Unit generates *pᵃ_t* incrementally to trace the input tokens from left to right (Mode 1). Then, the Mode 2 pointer *pᶜ_t* is computed using attention to find the token with the same ID, which becomes the output at step t. Without Mode 2 access, PANM would fail to perform this task. Source.

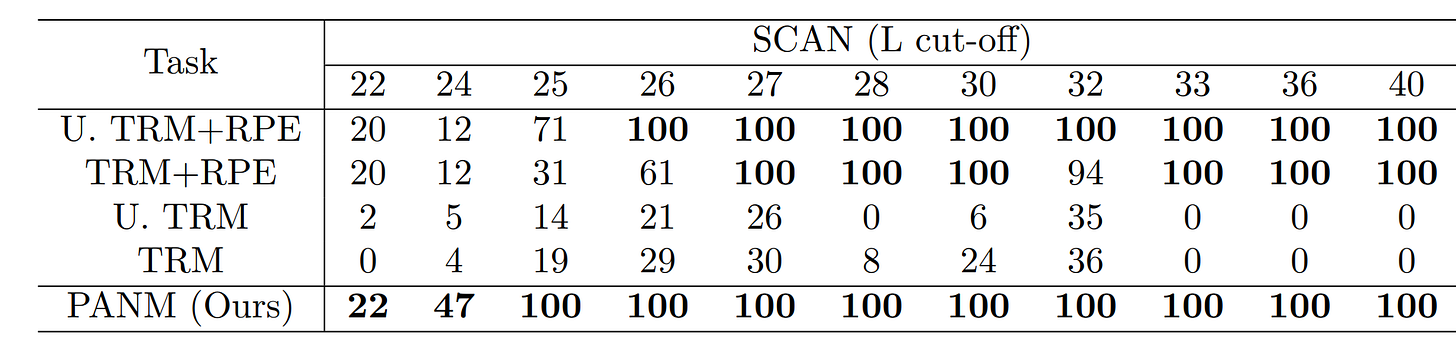
Another task requiring pointer manipulation is compositional learning. For example, the SCAN benchmark tests a model’s ability to map input sentences into sequences of commands [4]. The sequences are compositional, meaning they consist of reusable parts. For example, the input "jump twice" should map to "JUMP JUMP," and "walk twice" to "WALK WALK."

A challenging version of SCAN is the length split, where the training sequences are shorter than the test sequences. In this setup, test sequences range from lengths 22 to 40. The paper evaluated ChatGPT on this version by providing 20 in-context examples from the L-cutoff=40 split (the easiest setting) and testing it on 10 unseen sequences.

ChatGPT completely failed the task, achieving 0% exact match accuracy, even when tested on sequences similar in length to the provided examples. Below are a few examples of its errors:

Input: "walk and turn opposite right"  

ChatGPT output: "I_TURN_RIGHT I_TURN_RIGHT I_WALK"  

True output: "I_WALK I_TURN_RIGHT I_TURN_RIGHT"

Input: "run around left twice and run around right"  

ChatGPT output: "I_RUN I_TURN_LEFT I_RUN I_TURN_LEFT I_RUN I_TURN_RIGHT I_RUN"  

True output:  

  "I_TURN_LEFT I_RUN I_TURN_LEFT I_RUN I_TURN_LEFT I_RUN I_TURN_LEFT I_RUN  

   I_TURN_LEFT I_RUN I_TURN_LEFT I_RUN I_TURN_LEFT I_RUN I_TURN_LEFT I_RUN  

   I_TURN_RIGHT I_RUN I_TURN_RIGHT I_RUN I_TURN_RIGHT I_RUN I_TURN_RIGHT I_RUN"

These errors demonstrate the difficulty of length extrapolation, or the ability to generalize to longer sequences—a key challenge that SCAN is designed to evaluate. Compared to Transformer-based methods, PANM shows much better generalization on this task, across length cut-off splits.

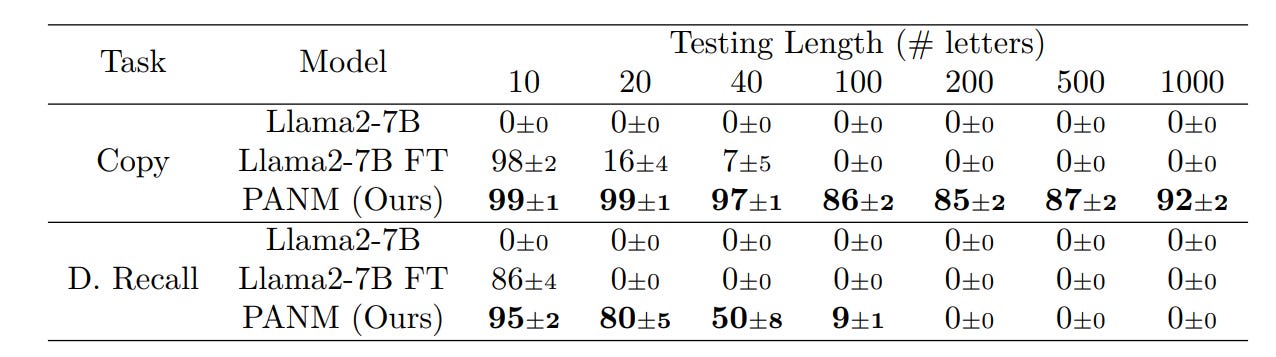
Finally, on LLM benchmarks, the papers show that even LLMs like Llama-2, when finetuned on task data, still struggle with length extrapolation. In particular, after being fine-tuned, the LLMs are given the prompts corresponding to the tasks:

The challenge is that the testing sequence in the testing prompt is much longer than those seen in the fine-tuning datasets. When the LLM is augmented with PANM, we are building a Memory-Augmented LLM where PANM plays the role of working memory and LLM is the controller.

The combination of PNAM and LLM Llama2 makes the performance better, as shown below:

Nevertheless, the overall performance of all tested methods remains low, indicating opportunities for improvement in future work.

Appendix

How Efficient is the Base Address Sampling?

A natural concern with base address sampling is whether exposing all possible addresses during training would require a large amount of data. However, we can show that the complexity is small compared to standard training procedures, making it a practical and efficient approach.

Let’s assume:

The training sequence length is L.
The maximum address range the model can handle during testing is L_max.
We define n=L_max/L as the ratio of the maximum address range to the training sequence length.

In cases where the maximum sequence length L_max→∞, the problem can be formulated as a Coupon Collector's Problem. The expected number of samples required to expose all addresses at least once is:

\(O(n \log n) \quad \text{where} \quad n = \frac{L_{\text{max}}}{L} \)

This result shows that the number of required samples grows sublinearly with respect to the address space, making it manageable even for large ranges.

👀 Consider an extreme case where L_max=10⁶ (though such a large range is rarely needed in practice) and the input sequence length is L=10 In this scenario, the number of samples required to expose all addresses becomes:
\(n \log n = 10^5 \log 10^5 \)
This amount of data is often smaller than typical dataset sizes, meaning the cost of base address sampling remains practical even under large address ranges.

Differences Between PANM and Transformers or Softmax Pointers

Pointers in neural networks are not a new concept. Indeed, pointers have been used in neural networks for quite some time, especially in models designed for sequence-to-sequence tasks. However, the way pointers are employed in these models can vary significantly.

In traditional pointer networks, a “softmax pointer” mechanism is often used to attend to elements in the input sequence. This mechanism is typically implemented using a combination of attention and a softmax function. The softmax function assigns probabilities to each element in the input sequence, and the element with the highest probability is selected as the pointer's target. Softmax pointers are common in Pointer Networks or Transformers.

To understand the major difference between explicit pointers and “softmax“ pointers, we can refer to the table below:

Summary of the difference between PANM’s pointers and softmax pointers. Source.

Overall, by incorporating explicit pointers into the neural network architecture, PANM introduces a novel mechanism that can enhance the model's ability to extrapolate sequences to varying lengths. This capability is particularly beneficial for tasks that require reasoning over sequences of varying sizes, such as question answering, summarization, and text generation.

References

[1] Maxwell Nye, Armando Solar-Lezama, Josh Tenenbaum, and Brenden M Lake. Learning compositional rules via neural program synthesis. Advances in Neural Information Processing Systems, 33:10832–10842, 2020.

[2] Oriol Vinyals, Meire Fortunato, and Navdeep Jaitly. Pointer networks. Advances in neural information processing systems, 28, 2015.

[3] John Von Neumann. First draft of a report on the edvac. IEEE Annals of the History of Computing, 15(4): 27–75, 1993

[4] Brenden Lake and Marco Baroni. Generalization without systematicity: On the compositional skills of sequence-to-sequence recurrent networks. In International conference on machine learning, pp. 2873–2882. PMLR, 2018.

[5] Le, Hung, Dung Nguyen, Kien Do, Svetha Venkatesh, and Truyen Tran. "Plug, Play, and Generalize: Length Extrapolation with Pointer-Augmented Neural Memory." Transactions on Machine Learning Research, 2024.

Neurocoder Tales

Discussion about this post