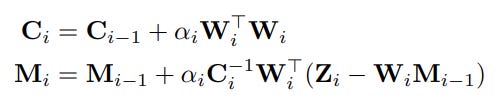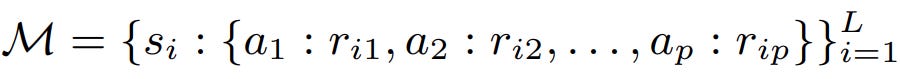Table of Content
What are Memory-Augmented Neural Networks?
Memory is the essence of intelligence. Thanks to memory, humans can recognize objects, recall events, plan, explain, and reason. It allows us to learn continuously, adapt to new environments, and apply past knowledge to unfamiliar situations. For AI, memory could be equally transformative. In neural networks, memory enables more than just storing patterns—it provides a way to connect past experiences to current tasks, to adapt across contexts, and to hold knowledge over time [1].
A Brief History of MANNs
Integrating memory into neural networks is not a new concept—it dates back to early models like recurrent neural networks (RNNs) and the Hopfield network, which introduced the idea of internal state retention. In these architectures, memory is embedded within the hidden states of the networks, allowing them to process sequences and retain a limited context. For example, classic RNN memory reads:
where ht is the hidden state or memory at step t. Here, xt is encoded in the current memory and ht-1 represents the previous memory capturing previous inputs x1, x2, …, and xt-1.
Long Short-Term Memory (LSTM) networks further developed this idea, adding mechanisms like gates to control memory flow and enable long-range dependencies. However, these internal states are still limited in how effectively they can store and retrieve large amounts of past information.
👀 The vector memory ht fails to scale up when the number of dimension increases since Wh would require much more parameters, much bigger memory and is much slower to learn or compute. Therefore, vector-based memory is often low in capacity.
It was only with the development of memory-augmented neural networks (MANNs), such as Neural Turing Machines (NTM, [2]) and Differentiable Neural Computers (DNC, [3]), that memory became a specialized and external component of the model. Unlike RNNs, which are constrained by the fixed size of hidden states, NTMs, and DNCs use a matrix memory that allows the network to store vast quantities of data explicitly. This matrix memory functions like a writable memory bank, consisting of multiple slots, where information can be stored, retrieved, and updated independently, providing a dedicated structure for past knowledge. The role of memory in these models became clearer: it was not just a transient internal state but a long-term storage that could be accessed flexibly. Given previous input tokens, a Controller, which later becomes LLM, is trained to read, write the memory, and make predictions on the next tokens:
In MANNs, the matrix memory M can be updated recursively as the hidden states of RNNs:
where f is a general update function, which depends on the memory architectures and designs.
MANNs with matrix memory are now a promising direction for building neural networks with human-like memory capabilities. In these systems, memory is external to the network and accessed via learnable controllers, enabling the model to decide what to write and read from memory based on task needs. A complete memory model can capture both past data and relationships between data, resulting in a deliberate reasoning system that can simulate high-order reasoning [4].
Thus, the MANN approach allows for complex reasoning, long-term dependencies, and the handling of variable-length sequences, bringing neural networks closer to the adaptive and context-aware memory found in human cognition.
What's Holding Back MANNs?
While powerful, Memory-Augmented Neural Networks (MANNs) face key obstacles. First, their complex memory operations introduce high computational costs, making them slow and challenging to scale with large datasets. Let’s have a look at the write operator of the DNC memory to understand why:
where w, e, v are neural network functions, ⊙ and ⊗ are Hadamard (element-wise) and outer product, respectively.
MANNs also require a sophisticated controller to decide when and how to read from or write to memory. Training this controller is difficult, as no labeled steps guide memory access decisions. Without ground-truth reasoning labels, the controller must learn these strategies from scratch, a challenging process akin to meta-learning that can make training unstable and slow.
Finally, truly memory-demanding tasks are rare, and limited real-world data naturally requires such complex memory operations. This scarcity of relevant training data limits opportunities to unlock MANNs' full potential, holding them back from broader applications.
👀 The limitations outlined above highlight why, despite numerous Memory-Augmented Transformer designs, few are practical or capable of scaling to billion-parameter LLMs.
The Rise of Memory in the LLM Era
Things change when LLMs emerge. In the evolving landscape of AI, memory, and LLMs form a symbiotic relationship, each enhancing the capabilities of the other. This interdependence allows both memory and LLMs to reach their full potential, making them far more powerful together than when used independently, heading towards Artificial General Intelligence (AGI).

Why Memory Craves LLMs?
By leveraging vast amounts of pre-trained knowledge, LLMs can significantly reduce the reliance on task-specific data, making training memory models for memory-intensive tasks more feasible. Moreover, LLMs are sophisticated enough to act as controllers, managing memory access more intuitively and efficiently. This eliminates the need for complex, manually trained controllers, streamlining the training process.
LLMs with memory are also faster and more efficient. LLMs can access and store information quickly by integrating memory within the model architecture, reducing computational overhead. This makes them more scalable and suitable for handling large datasets and complex reasoning tasks.
Ultimately, LLMs provide a natural and efficient way to integrate memory into AI systems. Their inherent capacity for learning and adaptation allows them to seamlessly incorporate memory mechanisms, enhancing their ability to process long-term dependencies and generalize across tasks.
Why LLMs Thrive with Memory?
LLMs are powerful tools, but they often struggle with tasks that require long-term context or reasoning over multiple steps. This is where memory comes into play. By integrating memory mechanisms, LLMs can:
Handle Long-Term Dependencies: LLMs can remember and utilize information from earlier parts of a text or conversation, improving their ability to generate coherent and contextually relevant responses.
Facilitate Complex Reasoning: Memory allows LLMs to store intermediate results and refer back to them as needed, enabling more sophisticated reasoning processes.
Enhance Creativity and Originality: LLMs can generate more creative and original content by accessing a vast knowledge base. Memory enables them to combine ideas from different sources and generate novel outputs.
By addressing these limitations and harnessing the power of memory, LLMs can become even more versatile and capable, opening up new possibilities for AI applications.
Theoretically, we cannot prove that a pre-trained LLM is computationally universal, meaning it can solve any computable problem or simulate a universal Turing Machine. This limitation arises because LLMs are trained on finite data, and their convergence after training cannot be guaranteed to meet the conditions of universality. However, by equipping an LLM with external memory, it can achieve computational universality under reasonable assumptions [5].
Now, you may ask 🧠 what is a universal Turing Machine? A Turing Machine (TM) is a theoretical computing model that can solve any computable problems given infinite memory. However, one TM only solves one specific problem. Universal Turing Machine (UTM) can simulate any TM given that the TM description is provided as the input. Therefore, one UTM, in theory, can solve all computable problems. UTM is realized as a general-purpose computer today, where the memory of the computers stores both programs and data.
👀 UTM can be simulated approximately using neural network architectures that are trained end-to-end [6].
The guarantee that an LLM with external memory can compute anything is significant, as it suggests that external memory can enhance LLM performance on complex tasks.
Memory-Augmented Large Language Models (MA-LLM)
Previous sections show that memory is vital in transforming LLMs from powerful tools into truly adaptive and intelligent systems. 🧠 But what kind of memory is suitable for LLMs? Just as the human brain relies on both working memory and episodic memory to navigate the world, LLMs benefit from these complementary forms of memory to handle diverse and complex challenges.
👉Working memory in LLMs is a short-term storage system, holding information relevant to the current task. Like a notepad for a writer, it is cleared and reset when the task concludes, making room for new data without interference from prior activities. This ensures that LLMs remain focused and efficient, adapting quickly to new tasks without being overwhelmed by the past.
In contrast, 👉episodic memory provides a longer-term perspective, capturing and storing knowledge that spans multiple tasks and events. It acts as a journal, retaining experiences, decisions, and outcomes, which can be revisited to improve understanding and performance over time. Episodic memory allows LLMs to learn from prior interactions and carry forward context, fostering continuity and depth in tasks requiring cumulative reasoning or personalized responses.
Working Memory
The bounded input length of LLMs, such as the typical 4096-token limit, restricts their capacity to handle complex, multi-step reasoning tasks. Augmenting LLMs with external read-write memory offers a promising solution by extending their computational abilities and enabling them to simulate algorithms beyond the scope of finite automata. This external memory acts as a working memory, dynamically storing intermediate computations, sub-problems, or task-specific data that can be retrieved and updated during a reasoning process.
Two key operators of working memory are:
Read Operator: Retrieves relevant information based on the current input and stored entries.
Write Operator: Updates the memory with new information generated during the task for future reference.
👀The working memory is often associative, in that it reads the data for the LLM based on the similarity of the current input and what is stored in the memory. Hence, it is also referred to as 👉associative memory.
String Memory: Enabling LLMs to Simulate Universal Turing Machines
A natural question arises: 🧠 What gets stored in the memory? One straightforward implementation is text—the memory can simply store raw text generated by the LLM or provided by users. This simplicity is sufficient to achieve universal computational capability, i.e., it can simulate a universal Turing Machine [5]. In the paper, the authors chose U15,2-a well-known small Universal Turing Machine as the simulation target. The U15,2 Turing Machine with a memory tape of an infinite number of slots can be described as follows:
States (Q): A finite set of possible configurations the TM can be in. In this case, U15,2 has 15 states, denoted as: {A,B,C,…,I,J}.
Tape Alphabet (Σ): A finite set of symbols that can be written on the tape. U15,2 has Σ={0,1}
Blank Symbol (b): A special symbol used to represent empty tape cells. Here, b=0
Start State (q₀): The initial state of the TM. q0=A
Halting States (T): A set of (state, symbol) pairs that, when reached, halt the TM. T = {(J, 1)}.
Transition Function (f:Q×Σ→Σ×{−1,+1}×Q): A function that, given a current state and the symbol under the tape head, determines:
The symbol to write to the tape.
The direction to move the tape head (left -1 or right +1).
The next state to transition to.
The transition function or program of U15,2 can be represented as a lookup table:
A Turing Machine starts in its initial state, reads the symbol under its tape head, and then, based on the current state and symbol, writes a new symbol, moves the head left or right, and transitions to a new state. This process repeats until the machine reaches a halting state.
Back to the contribution of the paper, the authors aim to simulate U15,2 using LLM augmented with a string-based memory.
👀The LLM is like a CPU that can access the working memory (RAM) to fetch data and instructions.
The memory functions as a dictionary, mapping keys (variable names or addresses) to values: MEMORY[variable name] = "value". Unlike physical RAM, keys are strings for seamless interaction with the LLM, while values can be either strings or integers. Following the UTM principle, the string values can also be the instructions. For example, MEMORY[‘op‘] represents the current instruction, eg., ‘halt‘. Other important memory variables are:
MEMORY[‘i‘] represents the current location of the Turing machine head. For example, MEMORY[‘i‘] =4 means the head is in the 4th slot.
MEMORY[number] represents the value stored at the number-th slot where the number is a string representing a number. For example, MEMORY[4] = ‘0‘, indicating the symbol stored in the 4th slot is ‘0‘.
With that in mind, the LLM system executes in 3 steps:
Read: Retrieve and construct the next input prompt from the memory
Compute: Execute the prompt (instruction) using the LLM
Write: Parse the LLM's output to extract variable assignments, store them back in memory, and move to step 1.
👀Notably, this approach requires no additional training or weight modification of the LLM, relying purely on prompt engineering and memory management for universal computation. The authors can test this approach on Flan-U-PaLM 540B.
To guarantee computational universality stems from the system itself, interactions between the LLM and memory through Read and Write are limited to finite-state operations, like simple regular expression parsing. It is important to verify the power of LLM+String Memory to see if it is truly computational universality. Otherwise, during computation, the system can query another computer for answers. Now let’s look at each step in detail.
Read
The processing rule with the memory should be defined and executed by simple Python programs. For example, given a string, we can do Read by replacing the variable name that appears in the string (e.g., like @[variable_name]) with the value stored in the memory whose key equals the variable name:

Given this function, any string containing pattern char[] can be replaced by memory content easily.
Compute
In this step, the LLM tries to perform the U15,2’s transition function above. It is provided with the string representing the current state and the program that reads like:
if the current head value on the tape is 0, the state will become B, write 0 to the current head, and shift the head right …
We are asking the LLM to do if-else generation conditioned on the head value using an instruction prompt. 🧠 How to design the prompt? The authors propose to use few-shot instruction to help the LLM familiarize with the syntax of generation output and if-else behavior. Some examples read:
result = " op="%[B]" %[i]="0" i+=1 "
if 0==1 then result = " op="%[A]" %[i]="1" i+=1 "
$result
" op="%[B]" %[i]="0" i+=1 "result = " op="%[B]" %[i]="0" i+=1 "
if 1==1 then result = " op="%[A]" %[i]="1" i+=1 "
$result
" op="%[A]" %[i]="1" i+=1 "All examples are stored in a variable boot stored in the memory. In other words, MEMORY[‘boot’] = “result = " op="%[B]" %[i]="0" i+=1 …".
Each transition rule corresponds to a state instruction prompt coupled with the few-shot examples. Each prompt is stored in the MEMORY as variables A, B, C …
A = """@[boot]result = " op="%[B]" %[i]="0" i+=1 "
if @[@[i]]==1 then result = " op="%[A]" %[i]="1" i+=1 "
$result
"""
B = """@[boot]result = " op="%[C]" %[i]="1" i+=1 "
if @[@[i]]==1 then result = " op="%[A]" %[i]="1" i+=1 "
$result
"""
...For example, if the current state is A, MEMORY[‘op‘] =
"""@[boot]result = " op="%[B]" %[i]="0" i+=1 "
if @[@[i]]==1 then result = " op="%[A]" %[i]="1" i+=1 "
$result
"""
and we give that prompt to the LLM after loading the value head @[@[i]] from the memory using Read. For example, let's say the value is 1, then we expect that the LLM will generate: op="%[A]" %[i]="1" i+=1
Write
Given LLM’s raw output, we need to substitute the variable name (%[variable_name]) with its values stored in the memory, producing a post-processed output string. Then, the authors use a simple Python program to update the memory values with the assignment specified in the output string.
Putting together, the whole system simulating U15,2 looks like this:
# Step 1: Initialize memory with predefined variables and values
Initialize MEMORY with:
'boot', 'i', 'A', 'B', ... (values are defined earlier)
# Step 2: Set the initial operation
MEMORY['op'] = MEMORY['A'] # Start with operation defined in 'A'
# Step 3: Main execution loop
While True:
op = MEMORY['op'] # Get the current operation
# Check if the process should stop
If op == 'halt':
Exit loop # End the program
# Perform core actions
Read # Fetch required data
Compute # Perform calculations or operations
Write # Update memory
Despite being theoretically powerful, the design of this kind of string memory faces difficulties:
❌ The system does not aim to solve the task directly. Rather, it simulates a UTM and then uses the program of the TM to solve the task. In theory, it can solve any task, but it still requires finding the program of TM that is suitable for the task. It is unclear how to find that program.
❌ Working on string or text level is slow because the LLM must generate texts and that involves a sequential sampling process, which is slow.
Tensor Memory: Long-term Storage and Generalization Power
In implementation, neural networks work with tensors. Therefore. it is convenient to store vector and tensor representations in the working memory, enabling the LLMs to communicate with LLMs in the representation-level, rather than text level. For example, Wang et al., (2024) proposed storing the LLM’s attention keys and values in external memory:
In particular, the input sequence is split into fixed-length (context_size) segments, each processed by a frozen LLM and their key-value pairs cached in memory. Current inputs use query vectors to retrieve memory content, fused with the local context for another trainable network (👉SideNet) to make predictions.
SideNet, implemented as a Transformer, uses the backbone LLM's embedding layer and frozen language modeling head:
The hidden state H will then be used to generate Q, K, and V to do the attention normally :
The catch is we will augment this attention with memory contents by a special memory retrieval and fusion.
Token-to-Chunk Memory Retrieval simplifies and accelerates memory operations by grouping tokens into fixed-size chunks. Instead of retrieving token-level key-value pairs, the system retrieves chunk-level pairs using mean-pooled vectors for efficient matching, then flattens the retrieved chunks back into token-level pairs for processing.
👀This approach reduces retrieval complexity, enhances accuracy, and allows adjustable granularity based on task needs, such as broader context for in-context learning.
Given the current token’s query, we can retrieve the top K/context_size chunks. After flattening the chunks, we obtain K key-value pairs as the memory contexts. Rewrite them in tensor form for all input token reads:
Memory Fusion combines local and retrieved memory contexts through a joint-attention mechanism in a specialized memory-augmented layer. Each token can attend to the tokens stored in the memory:
Then, we combine the memory attention with SideNet attention to produce the final output at layer l:
👀 During memory-augmented adaptation, only the SideNet's parameters are updated, while the backbone's pre-trained knowledge remains fixed. This streamlined method facilitates rapid convergence by effectively utilizing the existing expertise of the backbone model (405M GPT-2).
❌ The frozen LLM offers both advantages and drawbacks. While it keeps the system lightweight, it limits adaptability. For instance, if the pre-trained LLM has shortcomings, the quality of memory content may suffer, reducing the effectiveness of the augmentation.
❌ Chunk-level retrieval, while extending the memory span, cannot provide precise access to specific tokens, which limits its utility in applications requiring detailed reflection on past inputs, such as code generation or fine-grained question answering.
❌ The SideNet is trained to purely combine the memory content with its current input. This process relies on KNN retrieval without learning to read or write to the memory and offers no mechanism to ensure generalization.
To address these issues, we can consider a more flexible design where the memory can be differentiable:
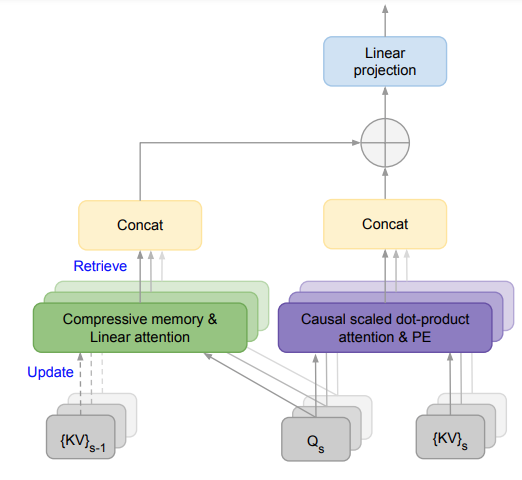
The proposed mechanism, termed 👉Infini-attention, also stores Q, K, and V representations of the LLMs. However, unlike Wang et al., (2024), the author proposes to use a compressive memory that adopts a recurrent update using Linear Attention [9]:
or Linar Attention combined with Delta rule:
Then, the memory read performs a normalized matrix multiplication:
Like Wang et al., (2024), this is interpolated with LLM’s original attention Adot:
👀 Each Infini-attention layer is trained via backpropagation through time using gradients of compressive memory states, similar to RNN training. This is expensive, yet allow better adaptiation to downstream tasks that requires finetuning LLM.
A different, more classical approach, for MA-LLM adopts the Controller Memory framework of NTM and DNC. In this MM-LLM architecture, the memory contains multiple slots. The LLM Controller reads and writes token representations to the slots. To save computation costs, the memory can be applied to the final layer of the LLM’s Transformer Encoder and Decoder as in Pointer-Augmented Neural Memory (👉PANM) [10]:

Unlike prior works that aim to use memory as long-term storage, PANM focuses on leveraging memory to empower LLM with length extrapolation capabilities. As such, PANM introduces a pointer-based mechanism with two principles:
Explicit Pointers as Physical Addresses: Incremental binary addresses replace softmax-based attention, ensuring scalable and predictable memory access for long sequences.
Decoupled Pointer Operations: Pointer manipulation is separated from input data, enabling abstract operations like copying or sorting independently of specific values.
Inspired by slot-based RAM, this design ensures reliable storage and retrieval across sequences of any length. The memory consists of:
An address bank (A)—a collection of binary memory addresses.
A Pointer Unit (PU)—a module that manipulates pointers to access memory efficiently.
👀 Apllying PANM to LLama-2 7B improves allows the LLM to generalize to a new sequence length 100 times longer than those seen in the training data. More details on PANM can be found in our previous blog post.
Episodic Memory
In deep learning and reinforcement learning, episodic memory refers to a memory mechanism that stores specific experiences or "episodes" for future reference. Unlike working memory, episodic memory can last longer, across tasks. These memories typically capture key events or knowledge in a task, in associative key-value pairs. For example:
Eiffel Tower — Paris
Friend’s DOB — 29/11/1995
9 AM yesterday — played soccer
A defining characteristic of episodic memory, distinguishing it from associative memories like semantic memory, is its ability to update or rewire associations rapidly. This is essential in the context of LLMs as although massive knowledge or facts have been embedded in the LLMs’ weights, they are more like semantic memory, and slow to update. This highlights the need for an additional storage mechanism that can rapidly adapt to new data or knowledge.

Rapid Knowledge Integration with Differentiable Memory
In recent work, Das et al., (2024) propose an MA-LLM named 👉Larimar that mirrors the hippocampus-neocortex interaction, where the memory rapidly captures factual updates as episodic memory, while the LLM encodes long-term patterns as semantic memory [11]. The episodic memory module serves as a global repository for storing the latest factual updates or edits, conditioning the LLM decoder to reflect this information.

Given a set of encoding Zi computed by the Encoder, representing the i-th knowledge we want to add to the memory M, assuming that we can find the address (key) W that specifies where to write to the memory, the authors propose the following memory update rule:
This rule resembles the Linear Attention + Delta Rule mentioned above. Furthermore, the memory update rule ensures important theoretical properties. Assuming Mi-1 is the least-squares solution for Z0:i-1:
We want to remember Zi, so we set αi=1:
Case 2: We want to forget Zi, which is stored before at iforget<i, so we set αi=-1:
👀 Intuitively, the least-squares solution results in a good memory because the memory is computed such as we can minimize the reconstruction error, i.e., we can optimally reconstruct past data Zj.
So far, we have assumed Wi is given. 🧠 How to compute Wi? The authors follow a prior work [12] in determining optimal values for Wi:
where X+ denotes the pseudo-inverse of X. Intuitively, the idea is still to minimize the reconstruction error. Given the memory, we can read or generate new content as follows:
Despite sound motivation for memory read/write design, Larimar has several drawbacks:
❌ The approach assumes no inherent order between episodes, neglecting temporal dependencies between knowledge across episodes. This limitation is evident in the memory update rule, where altering the order of Z does not affect the resulting memory values.
❌ Using pseudo-inverse operations to estimate memory and addresses can become computationally slow when the number of memory accesses is high.
❌ Training memory operations using backpropagation can be slow and require many training data samples.
To address the first limitation, Ko et al., (2024) propose to model the temporal dependencies between facts. This is critical for QA tasks that require advanced reasoning:
The proposed method, dubbed 👉MemReasoner leverages Larimar memory operations:
Furthermore. it introduces 2 new components:
Temporal Encoding: Positional encodings are computed for each line of context using sine and cosine functions. Additionally, learnable encodings are explored using a bidirectional GRU, where input sequences generate ordered context embeddings through GRU outputs. These embeddings are then written to memory using Larimar’s write operation.
Multi-step Reasoning with Query Rewriting: Multi-step reasoning tasks involve iterative "hops" between facts until the solution is reached. At each hop, zq is processed by a simple linear transformation to align with memory content:
\(\hat{z}_q = W_q z_q\)Like Larimar, the memory readout is computed as:
The query is updated iteratively:
This new query will be used to get a new read value z’r. This continues until convergence, i.e., ||zr-z’r||<τ or after a maximum number of iterations.
👀 Query rewritting is crucial when it requires multiple readings from the memory to find the relevant fact. For example, the orignial query is about A, and we want to know about E. If A-B, B-C, C-D, D-E facts are stored in the memory, we would need 4 reading “hops“.
Prompt Optimization with Nearest Neighbor Memory
An efficient way to enhance LLM performance is by refining the prompting process. Episodic memory can significantly improve prompt optimization, benefiting the LLM's outputs as effectively as augmenting the model itself.
By treating each training instance as an episode, the memory archives the experience of a seen prompt, which consists of input data, in-context learning (ICL) examples, and corresponding performance. During testing, we can refer to past experiences stored in the memory, to construct the prompt that potentially maximizes the testing performance.
Based on this principle, Do et al., (2024) propose an episodic memory for in-context example ordering optimization, called 👉POEM [14]. In their paper, the memory M is a set of tuples:
where s, a, and r are state, action, and reward, inspired by reinforcement learning notations and L is the size of the memory. In the context of LLM, they mean:
State s: the input data, i.e., the question we want the LLM to answer
Action a: the ordering of the in-context examples given we know the in-context examples
Reward r: the accuracy of the LLM’s output when prompted with (s, a)

The paper models these components as follows:
State representation: SentenceTransformer is used to encode the input to a state vector
Example selection: The set of examples is simply selected using a nearest neighbor search on a given database. We do not need to optimize this process.
Action encoding: The authors propose a clever way to allow generalization by representing the arrangement of in-context examples as a sequence of similarity ranks rather than their actual content. This rank-based representation captures relationships between examples, reducing overfitting and allowing the system to adapt better to new queries.

👀 This action encoding scheme allows discrete action space, which is convenient for later memory reading.
Reward design: The reward changes depending on the tasks:
Exact Match: A reward is given if the LLM’s output perfectly matches the ground-truth answer:
Classification: The reward is the difference between the log probability of the correct class and the largest log probability of the other classes:
Generation: The reward is the difference between the log probability of the ground-truth sequence and the largest log probability of other sequences:
While building the memory, we sample the data—the state, from the training data, select the in-context examples, and explore possible actions—the ordering of in-context examples to construct the complete prompt. The prompt will be used for LLM to generate outputs and collect the rewards. Given the tuple (state, action, reward), POEM defines memory operations:
Memory writing: there are 2 scenarios:
If the state-action pair is new to the memory, we just insert the tuple into the memory. If memory is overflow, the oldest tuple will be removed
If the state-action pair already exists in memory, we update its stored reward to the current reward if the latter is higher. This maintains an optimistic estimation of the reward for the state-action pair.
Memory reading: We aim to estimate the value for taking action a for a new testing input st using nearest neighbor estimation with the state as the query:
where si, i = 1, ..., k are the k states with the highest similarity to the testing state st. CS is the Cosine Similarity measurement. The action that has the highest value estimation will be deemed optimal for the input st:
👀 The proposed approach is fast to train and do inference. The authors show that it works for an array of LLMs from e RoBERTa-large to Llama2-7B, 13B and 70B.
The Future of Memory
As LLMs continue to scale, integrating efficient memory mechanisms becomes critical for handling dynamic knowledge updates, long-term dependencies, and computational efficiency. Traditional transformer-based architectures face challenges in managing memory due to their quadratic complexity and reliance on attention mechanisms, which become computationally prohibitive for longer sequences. The future lies in fast, scalable memory mechanisms that exhibit linear complexity, parallelizability, and the capacity to manage long-term knowledge without degrading performance. Below, we highlight promising approaches shaping this evolution.
1. State Space Models (SSMs)
State Space Models represent a paradigm shift in sequence modeling. By combining linear state-space equations with deep learning, SSMs can efficiently process sequences with linear complexity. They inherently model long-range dependencies by operating in continuous time, making them well-suited for extending memory capabilities in LLMs. Their attention-free nature allows scalable memory management while retaining interpretability and robustness. Big SSMs such as Mamba have shown potential as a Transformer-based LLM alternative (see more in this blog post).
2. Linear Attention
Linear attention mechanisms reformulate traditional attention calculations to scale linearly with sequence length [9]. By approximating or reweighting the attention matrix using kernel methods or other simplifications, linear attention reduces the computational overhead without sacrificing the model’s ability to capture contextual dependencies. This method is inherently parallelizable and faster than standard self-attention, making it a practical choice for tasks requiring both speed and scalability. Linear attention also retains compatibility with existing architectures, providing an efficient path to extend memory capabilities.
3. xLSTM
xLSTM builds on traditional recurrent architectures, optimizing them for long-term memory retention and scalability [15]. Unlike vanilla LSTMs, xLSTM leverages architectural modifications to avoid vanishing gradients, allowing it to maintain information over extended sequences. It achieves near-linear complexity by avoiding redundant computations and parallelizing operations, making it a viable alternative for tasks requiring deep contextual understanding.
4. Stable Hadamard Memory Framework (SHM)
The Stable Hadamard Memory (SHM) framework employs the Hadamard product for memory updates and calibration, offering a robust and scalable memory solution [16]. Its core advantage is minimizing dependencies between time steps, stabilizing gradient flows, and preventing learning issues such as vanishing or exploding gradients. SHM is particularly adept at long-term reasoning, offering a linear complexity approach that is attention-free and inherently parallelizable.
Interestingly, these recent advancements converge under a unified Hadamard Memory Framework [16], where the matrix memory update process can be expressed in a linear formulation as:
For example,
SSM: M, C, and U are vectors
Linear Attention: Ct=1
xLSTM: Ct is a scalar
Viewing these advancements through a unified lens opens opportunities for comprehensive theoretical analysis and technical enhancements, offering valuable insights into the behavior and potential of modern attention-free LLMs. We will dive deep into this model in a separate blog post. Stay tuned!
Reference
[1] Le, Hung. "Memory and attention in deep learning." arXiv preprint arXiv:2107.01390 (2021).
[2] Graves, Alex. "Neural Turing Machines." arXiv preprint arXiv:1410.5401 (2014).
[3] Graves, A., Wayne, G., Reynolds, M. et al. Hybrid computing using a neural network with dynamic external memory. Nature 538, 471–476 (2016).
[4] Le, Hung, Truyen Tran, and Svetha Venkatesh. "Self-attentive associative memory." In International conference on machine learning, pp. 5682-5691. PMLR, 2020.
[5] Schuurmans, Dale. "Memory augmented large language models are computationally universal." arXiv preprint arXiv:2301.04589 (2023).
[6] Le, Hung, Truyen Tran, and Svetha Venkatesh. "Neural Stored-program Memory." In International Conference on Learning Representations (2020).
[7] Wang, Weizhi, Li Dong, Hao Cheng, Xiaodong Liu, Xifeng Yan, Jianfeng Gao, and Furu Wei. "Augmenting language models with long-term memory." Advances in Neural Information Processing Systems 36 (2024).
[8] Munkhdalai, Tsendsuren, Manaal Faruqui, and Siddharth Gopal. "Leave no context behind: Efficient infinite context transformers with infini-attention." arXiv preprint arXiv:2404.07143 (2024).
[9] Angelos Katharopoulos, Apoorv Vyas, Nikolaos Pappas, and Franc¸ois Fleuret. Transformers are rnns: Fast autoregressive transformers with linear attention. In International conference on machine learning, pp. 5156–5165. PMLR, 2020.
[10] Le, Hung, Dung Nguyen, Kien Do, Svetha Venkatesh, and Truyen Tran. "Plug, Play, and Generalize: Length Extrapolation with Pointer-Augmented Neural Memory." Transactions on Machine Learning Research, 2024.
[11] Das, Payel, Subhajit Chaudhury, Elliot Nelson, Igor Melnyk, Sarath Swaminathan, Sihui Dai, Aurélie Lozano et al. "Larimar: Large Language Models with Episodic Memory Control." ICML, 2024.
[12] Kha Pham, Hung Le, Man Ngo, Truyen Tran, Bao Ho, and Svetha Venkatesh. Generative pseudo-inverse memory. In International Conference on Learning Representations, 2021.
[13] Ko, Ching-Yun, Sihui Dai, Payel Das, Georgios Kollias, Subhajit Chaudhury, and Aurelie Lozano. "MemReasoner: A Memory-augmented LLM Architecture for Multi-hop Reasoning." In The First Workshop on System-2 Reasoning at Scale, NeurIPS'24. 2024.
[14] Do, Dai, Quan Tran, Svetha Venkatesh, and Hung Le. "Large Language Model Prompting with Episodic Memory." ECAI, 2024.
[15] Beck, Maximilian, Korbinian Pöppel, Markus Spanring, Andreas Auer, Oleksandra Prudnikova, Michael Kopp, Günter Klambauer, Johannes Brandstetter, and Sepp Hochreiter. "xLSTM: Extended Long Short-Term Memory." NeurIPS, 2024.
[16] Le, Hung, Kien Do, Dung Nguyen, Sunil Gupta, and Svetha Venkatesh. "Stable Hadamard Memory: Revitalizing Memory-Augmented Agents for Reinforcement Learning." arXiv preprint arXiv:2410.10132 (2024).