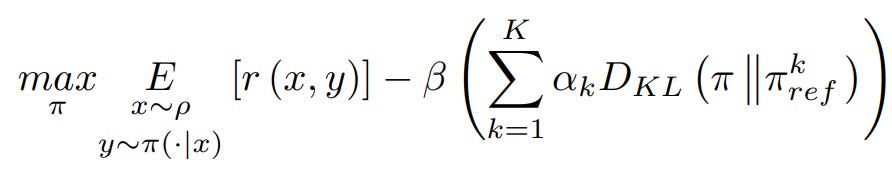Many Hands Make Light Work: Leveraging Collective Intelligence to Align Large Language Models

Multi-Reference Preference Optimization (MRPO) for Large Language Models (AAAI 2025)

Dec 10, 2024

For AI, Alignment Matters
- What is Preference Optimization?
- Direct Preference Optimization and Its Limitations
Enter MRPO: A Paradigm Shift
The Nuts and Bolts of MRPO
- Stable Alignment with Clipped Trust-Regions Optimization
- Automatic Reference Crediting with Adaptive Reference Weighting Coefficients
Key Achievements and Future Directions
- Performance with Limited Preference Data
- Scalability to Large Datasets
Appendix
Curiosity at the Mixer: Llama, Falcon, and Mamba Wondering What Happens Next! Source: Copilot.

For AI, Alignment Matters

In the rapidly evolving field of AI, alignment ensures that large language models (LLMs) generate accurate outputs and resonate with human values, preferences, and expectations. Without alignment, these powerful models risk producing content that may be misleading, offensive, or misaligned with user needs.

Imagine asking a language model for advice on a sensitive topic. Without proper alignment, the response might be factual but lack empathy, or worse, it could inadvertently reinforce biases or deliver information that feels detached or even offensive. Alignment bridges this gap, ensuring that these AI systems aren't just smart but also socially aware, user-focused, and culturally nuanced.

However, achieving alignment is no small feat. These models are trained on vast datasets spanning multiple domains and contexts. While this makes them incredibly versatile, it also means they can inherit biases or fail to understand the subtleties of human preference. For instance, if the training data primarily consists of texts about drills, the LLM may be biased towards generating related content, even when prompted to write about hammers.

AI can generate impressive outputs but may not always align with specific user intentions or preferences. Source: Copilot.

Without alignment, the sheer power of LLMs becomes a double-edged sword—capable of great innovation but also prone to generating content that's off the mark, misleading, or even harmful.

Preference optimization is a key technique in achieving this alignment—a process in machine learning that refines model outputs based on human preferences. It addresses the fundamental question: 🧠 How can we ensure AI aligns effectively with human judgment?

What is Preference Optimization?

Preference optimization is framed as the task of training a model f_θ, parameterized by θ, to align its outputs with human preferences derived from a labeled dataset D. The dataset typically contains tuples (x,y₁,y₂,…,y_n≻) where:

x represents a query or input
y₁,y₂,…,y_n are the outputs of the model
≻ is the preference label—it tells the order of preference between outputs, e.g., y₁ is preferred to y₂.

The roots of this technique trace back to classical frameworks like 👉learning to rank. For example, when we know the preference order y₁,y₂,…,y_n, we can train a scoring model with the learning to rank loss. This loss function ensures preferred items are ranked higher:

\(\mathcal{L}_{\text{rank}} = \sum_{i, j} \max(0, 1 - (s(y_i) - s(y_j))), \)

where y_i is preferred over y_j.

If we only have 2 outputs per data point, a common approach for comparing pairwise preferences is the 👉Bradley-Terry model. Here, we can model pairwise preferences probabilistically:

\(P(i \succ j) = \frac{\exp(s_i)}{\exp(s_i) + \exp(s_j)}, \)

where s is the score assigned to items i and j, respectively. This leads to the preference loss to learn the score function:

\(\mathcal{L}_{\text{pref}} = -\log \frac{\exp(s(y_1 | x))}{\exp(s(y_1 | x)) + \exp(s(y_2 | x))}, \)

In any case, given the scoring model, we can find θ such that:

\(\theta^* = \arg\max_\theta s(f_\theta(x)). \)

👀 By maximizing the score, the model f is aligning its output to satisfy the preference order provied in the dataset D.

Direct Preference Optimization and Its Limitations

To align LLMs, one can follow the classic framework:

Learn the scoring function
Optimize θ to maximize the score

However, this is slow and cumbersome due to the enormous size of LLMs. A recent breakthrough in this domain is 👉Direct Preference Optimization (DPO, [1]), a technique designed to improve LLM alignment without the complexity of the 2-step frameworks.

The core idea behind Direct Preference Optimization (DPO) is to fine-tune a language model using preference data from human feedback. A key aspect of DPO is using a reference model to constrain the updates made during fine-tuning. So the framework requires:

Optimize θ to maximize the score (without learning the score function explicitly)
Keep θ close to a reference model

Formally, we can write the original objective, often called Reinforcement learning from human feedback (RLHF), as:

where r is the score or reward model.

👀 This objective is hard to optimize, requring reinforcement learning.

The KL regularization balances the alignment with human preferences while retaining the base model’s general capabilities.

The DPO paper's main contribution is finding an alternative way to achieve the objective without learning r_ϕ. In particular, given:

The LLM π_θ we want to optimize
x represents a query, instruction, or input (see figure below)
y_w,y_l are the outputs of the model where y_w (chosen) is preferred to y_l(rejected)
A reference LLM π_ref

DPO derives a simpler objective to minimize the loss:

👀 This approach enables more efficient alignment of LLMs, as the closed-form loss can be directly minimized using gradient descent. Please refer to a detailed post on DPO and other related methods.

While this method ensures that updates remain within a reasonable range of the original model, it introduces significant limitations that hinder broader generalization and performance.

❌ Narrow Perspective. Using a single reference model inherently limits the diversity of knowledge and linguistic patterns available for fine-tuning. For instance, imagine teaching a language student by exposing them to only one teacher's style. While effective for consistency, this method misses the richness of perspectives that could arise from multiple sources.

❌ Overfitting to the Reference. A single reference model can inadvertently bias the optimization process, anchoring the fine-tuned model to the quirks or deficiencies of that reference. This risks overfitting to the reference rather than generalizing to a broader set of human preferences. For example, a translation model optimized using only one language corpus might struggle with dialects or rare syntactic structures.

❌Inefficiency in Knowledge Utilization. Modern AI ecosystems are brimming with diverse pretrained models, each excelling in different domains or capturing unique linguistic patterns. Single-reference approaches fail to harness this collective intelligence, leaving a wealth of useful prior knowledge untapped

Given these limitations, it’s logical to explore preference optimization methods that leverage the strengths of multiple reference models rather than relying solely on one. This multi-reference approach offers a pathway to richer generalization and more robust alignment. In the upcoming sections, let’s delve into the proposed solution.

Enter MRPO: A Paradigm Shift

At first glance, the idea seems straightforward: simply incorporate multiple reference models into the optimization process. Let’s refer to this approach as 👉Multi-Reference Preference Optimization (MRPO, [2]) for now.

Key Idea: Leveraging Multiple Reference Models Efficiently

Before diving into the design specifics, we need to establish the key desired characteristics of such a method:

Leverage Multiple Reference LLMs: Naturally, the core goal is to combine the strengths and insights of multiple pretrained language models to improve alignment outcomes.
Maintain Efficiency: The training and testing costs should remain comparable to those of Direct Preference Optimization (DPO). This ensures the approach is practical and scalable for real-world applications.
Allow Flexibility: The framework should enable the use of reference models that are not necessarily of the same type or architecture. This ensures versatility and leverages the diverse capabilities of existing language models.

Although there are many ways to utilize multiple LLMs, constraints related to efficiency and flexibility (Conditions 2 and 3) rule out several common approaches:

Joint training of multiple LLMs: This is straightforward yet too expensive. Loading multiple LLMs and updating their parameters requires massive resources.
Reinforcement learning with multiple constrained objectives: While this could theoretically align models with diverse preferences, it is often slow, computationally expensive, and challenging to implement effectively.
Model merging via weight interpolation: Combining LLMs by interpolating their weights requires that the models share the same architecture and parameter space. This limits applicability and fails to accommodate diverse types of LLMs.
Ensembling multiple LLMs at inference: This method demands running multiple models simultaneously during inference, which is resource-intensive and impractical for large-scale applications.
Knowledge Distillation (KD): We can leverage KD to facilitate DPO optimization by aligning the base LLM while ensuring similarity between the optimized policy (student) and additional reference models (teachers, k>1). It is important to note that this approach requires sampling y from the primary policy during training to compute the KL divergence, which introduces computational inefficiency.

Ultimately, we aim for a framework that offers:

Multiple LLMs are employed inexpensively only during training. Yet, only one Base LLM is trained.
During testing, only the Base LLM is loaded and executed, similar to DPO

Compared to DPO, the MRPO framework should look like the following:

Why Is Efficient Multi-Reference Not Easy?

Designing an efficient multi-reference preference optimization framework is far from straightforward. The key challenge lies in formulating a meaningful objective function that integrates multiple reference models effectively. Let’s start with the original objective of preference optimization in the case we have multiple references:

It resembles the original RLHF formulation, but it includes additional KL divergence terms that act as constraints, ensuring alignment with K reference models π^k_ref. In this formulation, α represents the weight assigned to the constraint term. A larger α places greater emphasis on aligning the main model with the corresponding reference model, effectively assigning more credit to that reference and encouraging the primary LLM to remain closer to its distribution.

There are several naive optimization strategies:

Using 👉RLHF [3]: Direct optimization of the multi-reference objective using RL is highly complex due to the need to balance multiple constraints simultaneously. Each reference model introduces a distinct constraint, complicating the learning process and making it computationally intensive.
Summing DPO Losses: A simple summation of the Direct Preference Optimization (DPO) loss terms across multiple references. We can call it 👉Multi-DPO and the loss reads:
This approach lacks the necessary coordination to ensure that the combined influence of the reference models aligns with the overarching goal. Each DPO term operates independently, which can result in conflicting gradients or an inability to fully leverage the diversity of the references. For example, summing losses might outweigh some models that are easy to align while underutilizing others, leading to less diversity and suboptimal fine-tuning.
Averaging Reference Models: An alternative, naive approach is to compute a single reference distribution π_avg as the mean of multiple reference models’ distributions:
\( \pi_{\text{avg}}(y|x) = \sum_{i=1}^K\alpha_i \pi^k_{\text{ref}}(y|x), \)

Then the objective becomes:
\(\theta^* = \arg\max_\theta \mathbb{E}_{x,y \sim \mathcal{D}} \left[ r(x,y) - \beta D_\text{KL}(\pi_\theta \| \pi_{\text{avg}}) \right]. \)
which can be optimized using normal DPO. While this method (👉Mean Ref) simplifies the process, it does not guarantee the optimization of the original multi-reference objective. Moreover, Mean Ref forces the base LLM to align with the average of the reference models, effectively focusing on their centroid. This disregards the unique and potentially valuable distinctions each reference model brings, reducing the model's ability to fully capture the diversity and richness of their contributions.

This raises a key research question for MRPO: 🧠 How can we design an optimization framework that adheres to the RLHF objective while avoiding the complexity and inefficiency of reinforcement learning?

How MRPO Builds on DPO

The goal is to derive a closed-form solution for the multi-reference RLHF objective, as expressed above. However, the inherent nonlinearity of the KL divergence terms makes obtaining an exact closed-form solution intractable. To address this challenge, Le et al., (2024) introduce a surrogate objective that provides a tractable lower bound for the original multi-reference RLHF objective. The important result is that we can derive the closed-form solution for the lower bound.

👀 The closed-form solution follows a structure similar to the one in DPO. It introduces a representative reference model, called virual reference, which is computed as a “weighted inverse sum” of the individual reference models.

Implementation-wise, we often need to compute the log of the virtual reference’s probability. For the case K=2, we can rewrite the log of virtual reference as:

\( \log\tilde{\pi}_{ref} = \log\left( \frac{\alpha\pi^1_{ref}+(1-\alpha)\pi^2_{ref}}{\pi^1_{ref}\pi^2_{ref}} \right)^{-1}=\log\pi^1_{ref}+\log\pi^2_{ref}-\log(\alpha\pi^1_{ref}+(1-\alpha)\pi^2_{ref}) \)

Let’s look at the code for the case of chosen data y_w:

# reference model 1's log prob: reference_chosen_logps1
# reference model 2's log prob: reference_chosen_logps2
# Let's do the inverse mean in the log space
sumlog= reference_chosen_logps1+reference_chosen_logps2
# To ensure safe exponential, use the Log-Sum-Exp trick
c = torch.max(reference_chosen_logps1,reference_chosen_logps2)
logsum= c + torch.log(alpha*torch.exp(reference_chosen_logps1-c)+(1-alpha)*torch.exp(reference_chosen_logps2-c))
# virtual reference log prob
reference_chosen_logps = sumlog - logsum

Given the log of reference model for both chosen and rejected data, we can similarly derive the MRPO loss as DPO, which is surprisingly simple:

It closely resembles the loss function used in DPO, with the key difference being that it substitutes the individual references with a virtual reference. This virtual reference is a weighted inverse combination of the multiple reference models. If you're interested in the detailed proof and derivations, be sure to check out the end of this post for a thorough breakdown.

👀 Interestingly, by using an "inverse mean" instead of the standard mean, MRPO is theoretically guaranteed to optimize a lower bound of the RLHF objective. This contrasts with the "Mean Ref" approach, which doesn't offer the same theoretical guarantee.

Even better, MRPO loss is theoretically better than naive variants such as Multi-DPO loss. This is demonstrated in the proposition:

Looking at the inequalities, we see why the MRPO loss is designed to outperform naive approaches like the Multi-DPO. In particular, MRPO behavior dynamically adapts to the accuracy of reward estimations:

Incorrect Reward Estimations (d_k>0): When the reward estimates are incorrect, MRPO produces a larger update magnitude than Multi-DPO. This accelerates the adjustment of likelihoods, helping the model quickly correct the implicit reward and improve alignment with the intended preference signal.
Correct Reward Estimations (d_k<0): Conversely, when reward estimates are accurate, MRPO applies smaller updates compared to Multi-DPO. This restrained adjustment can stabilize convergence and mitigate overfitting by preventing unnecessary large updates that might otherwise destabilize the optimization process.

This balance between aggressive correction and careful refinement ensures MRPO remains both responsive to errors and robust against instability, setting it apart from simpler multi-reference methods.

👀 MRPO is efficient in both training and inference. During training, the log probabilities of the data for reference (e.g., reference_chosen_logps1,2,…) can be precomputed, eliminating the need to load multiple LLMs. Once training is complete, inference requires loading only the Base LLM, further streamlining the process.

The Nuts and Bolts of MRPO

Despite being theoretically sound, there are potential challenges to applying MRPO:

❌ The mismatch between the reference and the main LLMs being trained

❌ Tuning the right reference weights α can be time-consuming. Moreover, a fixed value of α may be not optimal

In this section, we will explore ways to overcome these challenges

Stable Alignment with Clipped Trust-Regions Optimization

When using multiple reference policies in optimization, a key challenge emerges: the mismatch between the reference policies and the main policy being trained. In single-reference DPO, this issue is less pronounced because the main policy and the reference policy often originate from the same model, sharing similar architectures, tokenizers, and pretraining paradigms. This shared origin minimizes the likelihood of discrepancies in predicted probabilities, resulting in stable training.

However, when multiple reference policies come into play, the dynamics shift. Reference policies not used to initialize the main policy may diverge significantly in terms of probability distributions. These divergences can stem from variations in:

Architectures
Tokenization methods
Pretraining datasets

Wild Disagreement: Falcon, Llama, and Mamba in a Chaotic Clash. Source: Copilot.

Such discrepancies can introduce instability into the training process and, in extreme cases, cause the loss to diverge.

👀 Difference in probability scale can lead to numerical instability when computing logsum in the code above.

Despite these challenges, leveraging the diverse likelihoods provided by multiple references is critical for ensuring robust generalization. Diverse references capture a broader spectrum of possible outputs and preferences, enriching the training signal. 🧠 How can we do that while maintaining stability?

MRPO introduces Clipped Trust-Region Optimization (CTRO) to address the potential challenge. The core idea is to constrain the influence of each reference policy so that they remain within a reasonable "vicinity" of the initializing reference policy, denoted as π¹_ref. This ensures stability while preserving the benefits of diverse reference views. Mathematically, we clip the log probability of reference models around π¹_ref with a radius of ϵ :

\( \log \hat{\pi}_{\text{ref}, k>1}(y \mid x) = \min \left( \max \left( \log \pi_{\text{ref}, k>1}(y \mid x), (1 - \epsilon) \log \pi_{\text{ref}, 1}(y \mid x) \right), (1 + \epsilon) \log \pi_{\text{ref}, 1}(y \mid x) \right) \)

Looking deeper, a fixed trust-region size ϵ can be overly rigid because different policies and data points might require different levels of flexibility. For example:

High-confidence predictions (large log probabilities) suggest that the reference policy is reliable. In this case, updates should be cautious, meaning ϵ should be smaller.
Low-confidence predictions (small log probabilities) suggest uncertainty, where more exploration is warranted. Here, ϵ can be larger to allow for greater deviation.

To address this, MRPO employs an adaptive trust region where ϵ is determined dynamically based on x and y data. Thus, the formula for ϵ is:

\( \epsilon(y \mid x) = \epsilon_{\text{max}} \cdot \frac{ \left|\sum_{k=1}^K \log \pi_{\text{ref}, k}(y \mid x)\right| }{ \sum_{y'}\left| \sum_{k=1}^K \log \pi_{\text{ref}, k}(y' \mid x)\right| } \)

👀 Because probability is always smaller than 1, larger log probabilities means smaller absolute value of log probabilities, and vice versa.

Automatic Reference Crediting with Adaptive Reference Weighting Coefficients

When working with multiple reference policies in MRPO, it's essential to assign the right importance—or weights—to each one. A straightforward approach might be to assign equal weights to all references, assuming no policy is better or worse than another. However, this approach overlooks a crucial fact: not all reference policies are equally confident in distinguishing between correct (y_w) and incorrect (y_l) outputs.

MRPO introduces Adaptive Reference Weighting Coefficients (ARWC) to automatically assign the weight α_k to the reference models with potential benefits:

✔️ Reduce hyperparameter tuning effort

✔️ Aim for optimal credit assignment conditioned on input data

Imagine you’re judging a contest with multiple referees. If one referee consistently makes bold, confident decisions while another hesitates or frequently wavers, you’d naturally trust the confident one more. ARWC applies this intuition to weighting reference policies. It evaluates how decisively each policy differentiates between y_w (preferred output) and y_l (less preferred output) by examining the absolute difference in their log probabilities. A larger difference indicates higher confidence and thus assigns a higher weight to that policy.

Mathematically, the weighting coefficient for the k-th reference policy, α_k, is calculated as:

\(\alpha_k = \frac{\log \pi_{\text{ref}, k}(y_w \mid x) - \log \pi_{\text{ref}, k}(y_l \mid x)}{\sum_{i=1}^K \big( \log \pi_{\text{ref}, i}(y_w \mid x) - \log \pi_{\text{ref}, i}(y_l \mid x) \big)} \)

Here’s what each term means:

Numerator: Measures the confidence of the k-th reference policy by the log-probability difference between the preferred and less preferred outputs.
Denominator: Normalizes the weights across all reference policies so they sum to 1.

Let’s study an example to understand the formula. Picture this: You have 3 judges evaluating a math problem’s solution. Judge A gives a confident "10 out of 10" to the correct solution and "2 out of 10" to the incorrect one. Judge B is less sure, giving a "7 out of 10" and "6 out of 10," while Judge C is undecided, rating both solutions equally at "5 out of 10." ARWC ensures Judge A, with their stark differentiation, has the most influence in the final decision, while Judge C's lack of confidence reduces their weight.

Key Achievements and Future Directions

The paper evaluates MRPO with other multi-reference and single-reference approaches. The experimental setting follows:

LLMs Used:
- Llama-2-7b-chat-hf (L), OpenHermes-2.5-Mistral-7B (M), Qwen1.5-7B-Chat (Q). They examine different configurations of Base LLMs and Reference LLMs. In one experiment, Llama can be the Base, and Mistral can be the Reference. This setting is denoted as L ← M.
- Preference Optimization Method: Finetuned using LoRA 4-bit quantization on a Tesla A100 GPU.
Evaluation Metrics:
- Preference Learning:
  - Preference Accuracy: Ability to predict chosen vs. rejected responses.
  - Reward Margin: Quantifies reward differences between chosen and rejected responses.
- Helpfulness: Win Rate measured via GPT-4 evaluation.
- GLU Metrics: Average performance across various language tasks.

Performance with Limited Data (Small Datasets):

Datasets: S1, S2, S3 from public Hugging Face data.
Baselines: DPO (single reference), Multi-DPO, RLHF, Mean Ref, Knowledge Distillation (KD).
Results:
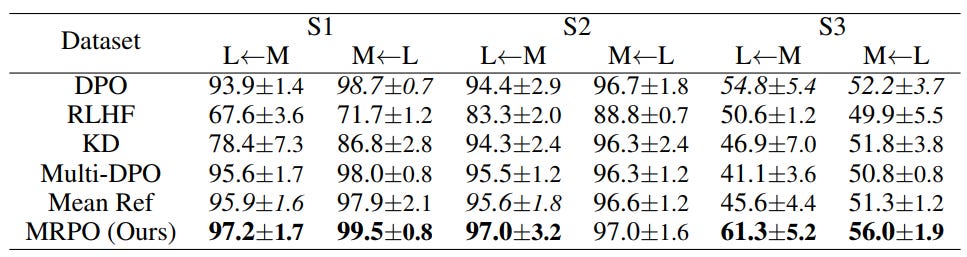
- MRPO outperforms DPO significantly:
  - L ← M: 3-7% improvement.
  - M ← L: 1-4% improvement.
- Comparison to Baselines:
  - RLHF underperforms due to optimization instability.
  - KD and Mean Ref struggles without theoretical support for alignment problems.
  - Multi-DPO, even with trust-region optimizations, often underperforms DPO and MRPO.

Scalability to Large Datasets:

Datasets: HelpSteer, Ultrafeedback, Nectar.
MRPO consistently outperformed DPO:
- Preference Accuracy: 3-5% (L ← M), up to 1% (M ← L).
- Reward Margin: 10-20% higher.

Dataset: HH-RLHF. Alpaca-Eval
MRPO outperformed DPO in win rate by 20-30%

Datasets include GSM8K (math), MMLU, TruthfulQA, etc.
MRPO (K = 3) improved performance over DPO by an average of 1.1-1.3%, with notable gains in tasks like GSM8K (+6.8%) and TruthfulQA (+5.8%).

While the Maximum Reward Policy Optimization (MRPO) framework presents a novel approach to improving policy alignment in Reinforcement Learning from Human Feedback (RLHF), it is not without its limitations:

❌ A key issue lies in its handling of policy-reference mismatches. Although clipping mechanisms are employed to mitigate excessive divergence between the policy and the reference models, they do not completely resolve the problem. This residual mismatch can lead to suboptimal updates, particularly in scenarios where the learned policy significantly deviates from reference models. On the other hand, the clipping mechanism in MRPO may not induce substantial changes to the underlying Base LLM.

❌ From a theoretical perspective, the current formulation of MRPO relies on a lower bound of the RLHF objective, which is not tightly constrained. The gap between the lower bound and the true objective value introduces uncertainty in the optimization process, potentially affecting the reliability of the learned policy. Additionally, MRPO does not provide an explicit method to estimate the error introduced by this bound, leaving room for further theoretical refinements.

Appendix

Below, we break down the mathematical derivation of the MRPO’s closed-form optimal policy.

The MRPO framework starts with an objective to maximize the expected reward while penalizing deviations from the reference policies:

\(\max_{\pi} \mathbb{E}_{x \sim \rho, y \sim \pi(\cdot|x)} \left[ r(x, y) \right] - \beta \sum_{k=1}^K \alpha_k D_{\text{KL}} \left( \pi || \pi_{\text{ref}}^k \right), \)

The objective is reformulated to minimize a weighted sum of log-probability terms (representing regularization) and the negative reward term:

\(\min_{\pi} \mathbb{E}_{x \sim \rho, y \sim \pi(\cdot|x)} \left[ \sum_{k=1}^K \alpha_k \log \frac{\pi_{\text{ref}}^k(y|x)}{\pi(y|x)} - \frac{1}{\beta} r(x, y) \right]. \)

Using Jensen's inequality:

\(\sum_{k=1}^K \alpha_k \log \frac{\pi_{\text{ref}}^k(y|x)}{\pi(y|x)} \leq \log \sum_{k=1}^K \alpha_k \frac{\pi_{\text{ref}}^k(y|x)}{\pi(y|x)}. \)

Thus, the upper-bounded objective becomes:

\(\min_{\pi} \mathbb{E}_{x \sim \rho, y \sim \pi(\cdot|x)} \left[ \log \sum_{k=1}^K \alpha_k \frac{\pi_{\text{ref}}^k(y|x)}{\pi(y|x)} - \frac{1}{\beta} r(x, y) \right]. \)

This approximation simplifies optimization while maintaining a valid lower bound for the original objective.

👀 Recall that we reformulate the original RLHF maximization objective as an equivalent minimization problem by negating it. Consequently, the upper bound of the minimization objective corresponds to a lower bound of the original maximization objective.

To ensure proper normalization of probabilities, a partition function Z(x) is introduced:

\(Z(x) = \sum_{y} \tilde{\pi}_{\text{ref}}(y|x) \exp\left(\frac{1}{\beta} r(x, y)\right), \)

where:

\(\tilde{\pi}_{\text{ref}}(y|x) = \left(\sum_{k=1}^K \alpha_k \frac{1}{\pi_{\text{ref}}^k(y|x)}\right)^{-1}. \)

The objective can be rewritten as:

\(\min_{\pi} \mathbb{E}_{x \sim \rho, y \sim \pi(\cdot|x)} \left[ \log \frac{\pi(y|x)}{\tilde{\pi}_{\text{ref}}(y|x)} - \frac{1}{\beta} r(x, y) - \log Z(x) \right]. \)

Using the Kullback-Leibler (KL) divergence, this becomes:

\(\min_{\pi} \mathbb{E}_{x \sim \rho} \left[ \text{KL}(\pi(y|x) || \pi^*(y|x)) - \log Z(x) \right], \)

where:

\(\pi^*(y|x) = \frac{1}{Z(x)} \tilde{\pi}_{\text{ref}}(y|x) \exp\left(\frac{1}{\beta} r(x, y)\right). \)

The KL divergence is minimized when:

\(\pi(y|x) = \pi^*(y|x). \)

Thus, the optimal policy is:

\(\pi(y|x) = \frac{\tilde{\pi}_{\text{ref}}(y|x) \exp\left(\frac{1}{\beta} r(x, y)\right)}{\sum_{y'} \tilde{\pi}_{\text{ref}}(y'|x) \exp\left(\frac{1}{\beta} r(x, y')\right)}. \)

From this point, one can refer to the DPO approach [1] to derive the MRPO loss.

Reference

[1] Rafailov, Rafael, Archit Sharma, Eric Mitchell, Stefano Ermon, Christopher D. Manning, and Chelsea Finn. "Direct preference optimization: Your language model is secretly a reward model." arXiv preprint arXiv:2305.18290 (2023).

[2] Le, Hung, Quan Tran, Dung Nguyen, Kien Do, Saloni Mittal, Kelechi Ogueji, and Svetha Venkatesh. "Multi-Reference Preference Optimization for Large Language Models." arXiv preprint arXiv:2405.16388 (2024).

[3] Christiano, P. F.; Leike, J.; Brown, T.; Martic, M.; Legg, S.; and Amodei, D. Deep reinforcement learning from human preferences. Advances in neural information
processing systems, 2017

Neurocoder Tales

Discussion about this post