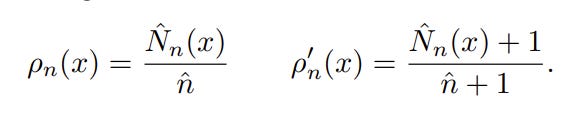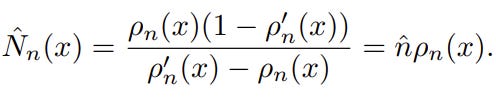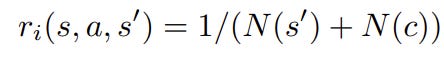In the preceding post, we studied classical exploration strategies primarily grounded in theoretical justifications under naïve assumptions, challenging to scale in complex scenarios. 🧠 Why is scaling a big problem? Practical environments often involve huge continuous state and action spaces, as exemplified below:
Doom environment: continuous high-dimensional state space (source).
Mujoco environment: continuous action space (source).
Classical approaches cannot be implemented or fail to hold their theoretical properties in these settings. Furthermore, primary exploration strategies in deep reinforcement learning face challenges in keeping up with the growing complexity of these expanding search spaces.
Interestingly, biological agents can cope with exploring vast continuous state and action spaces very well. For example, animals can travel long distances until they find food or water. Humans can navigate to an address in a strange city. Biological agents are less likely to solve for the UCB using Hoeffding's inequality. 🧠 What motivates these agents to explore? Before addressing this question, it is beneficial to explore the common framework of intrinsic motivations that propel agents to explore.
Primal approaches add entropy loss or inject noise into the policy/value parameters with the limitation that the level of exploration is not explicitly conditioned on fine-grant factors such as states or actions. One typical remedy is to use intrinsic reward bonuses, which assign higher internal rewards to state-action pairs that require higher exploration and vice versa. The final reward for the agent will be the weighted sum of the intrinsic reward and the external (environment) reward.
Reward bonus framework.
Exploration via intrinsic reward bonus.
In addition to bonus rewards, there are other methods to integrate intrinsic motivation into RL. For example, if we can identify the states that should be explored, we can use them as the goals in goal-conditioned RL approaches. We can also directly influence the policy towards the interesting states and actions by modifying the policy functions or the action sampling processes. Finally, in replay-based value learning, we can put more weight on the experiences that contain potential states and actions to encourage more visits to them. Among all, bonus reward is still the most common method due to its simplicity. Therefore, we will focus on this technique in this article.
Novelty
Humans want to explore novel places, make new friends, and buy new stuff. It is inherent for humans to be motivated by new things. 🧠 How to translate this intrinsic motivation to RL agents? Tracking the occurrences of a state (N(s)) provides a novelty indicator, with increased occurrences signaling less novelty. This can lead to an intrinsic reward structure resembling the UCB strategy: ri(s,a)=N(s)-0.5where N counts the number of times s appears. Unfortunately, relying on empirical counts in continuous state spaces is impractical due to the rarity of exact state visits, resulting in N(s)=0 most of the time. Correctly estimating N(s) demands additional effort. We can call such an estimation a pseudo-count.
State Counting
Bellemare et al. (2016) propose to use a density function of the state to estimate its occurrences, i.e., 👉density-based counting [1]. Let ρ(x)=ρ(s=x|s1:n) be a density function of the state x given s1:n and ρ’(x)=ρ(s=x|s1:nx) the density function of the state x after observing its first occurrence after s1:n . Assume the existence of N̂ (x) and n̂ as a “pseudo-count” of x and the pseudo-total count before and after an occurrence of s given previous states s1:n , respectively; because the true density of x stays the same before and after an occurrence of x, the following relationships hold:
which yields (by plugging n̂ value derived from the left to the right equation):
👀 In practice, in a huge state space, ρ’n(x)≈0, and thus we can rewrite the pseudo-count:
where PG means predictive gain, which is computed as:
This formulation closely resembles the information gain, which is the difference between the expectation of a posterior and prior distribution.
Now, the final task is to estimate ρ(s), which can be done using any density model such as CTS. After we get the pseudo-count, we can derive the intrinsic reward as follows:
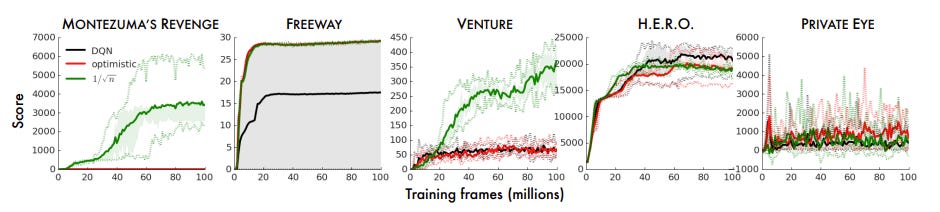
Here, the 0.01 term is to avoid dividing by zero when N̂ (x)=0. Using this reward, the authors improve DQN performance on various hard Atari games:
Exploration with pseudo-count (green line) on hard Atari games. Image taken from [1]
If counting each exact state is challenging, why not partition the continuous state space into manageable blocks? This is the approach taken by Tang et al. (2017) who use 👉hash count to address the counting issue [2]. By using a function 𝜙 mapping a state to a code, we can count the occurrence of the code instead of the state. 🧠 How to choose a good 𝜙?
One important choice we can make regards the granularity of the discretization: we would like for “distant” states to be counted separately while “similar” states are merged.
—Text taken from [2]—
The paper picks SimHash for the mapping function, and it is very simple to implement:
where sgn is the sign function, A is a k × d matrix with i.i.d. entries drawn from a standard Gaussian distribution. and g is some transformation function that maps the state space to a d-dimensional representation space. We can control the granularity of the discretization by setting the k value (higher k, less occurrence collisions, and thus states are more distinguished).
Further, Tang et al. (2017) propose an extension of the approach for high-dimensional state space. In particular, representation learning is employed to capture good g through autoencoder network and reconstruction learning:
Autoencoder architecture for training the representation g. Image taken from [2]
The network aims to reconstruct the original state input s, and the hidden representation b(s) will be used to compute g(s)=round(b(s)). In addition to the reconstruction loss, the authors introduce a regularization term during network training to binary-encode the representations. This prevents the corresponding bit in the binary code from flipping throughout the agent's lifetime. The final loss is defined as:
👀 Extending these counting approaches to count state-action pairs is straightforward. To measure the novelty of state-action combinations, one can concatenate the action representation with the state representation.
Change Counting
Concentrating solely on novel states or actions is useless when they have little or no impact on the outcome. In navigation tasks with diverse situations such as those in Minigrid, many activities are unnecessary:
For instance, moving around, bumping into walls, or trying to open locked doors without keys all result in no change and thus will be of low interest.
—Text taken from [3]—
To encourage the agent to explore novel state-action pairs meaningfully, we can assess changes caused by activities and prioritize those that signify novelty. In particular, we can define c(s,s’) as the environment change caused by a transition (s, a, s’) and use count-based methods to estimate its novelty. The proposed method, 👉C-BET, combines state count and change count, resulting in the intrinsic reward:
The authors recognize the effectiveness of counting both quantities rather than solely focusing on counting the states or using the norm of the change to represent novelty, as illustrated in the visualization:
Change count (last row) vs norm of change (middle row) vs state count (top row). Change count suffers less from attracting to meaningless activities. Image taken from [3].
❌ An inherent constraint of count-based methods lies in the approximation error between the pseudo-count and the true count. The sensitivity of counting is particularly evident in the choice of representation or density model, especially when two states may share similar representations but should not be considered the same when counting.
Novelty through Reachability
Another idea to overcome the limitation of count-based methods is to model novelty through different criteria. In [4], the authors provide an interesting intuition: novel observations are those that demand effort to reach, typically beyond the already explored areas of the environment. They measure the effort in environmental steps, estimating it with a neural network that predicts the steps between two observations. To capture the explored areas of the environment, they use an episodic memory initialized empty at the start of each episode and call their method 👉Episodic Curiosity (EC). Observations encountered during an episode are then added to this memory.
By assessing the reachability score in terms of the estimated number of steps between a given observation and all stored observations in the memory, we can gauge the novelty of the observation. For example, if the maximum reachability score of the given observation is greater than a threshold k, we can regard it as novel.
Novelty through reachability concept. An observation is novel if it can only reach those in the memory in more than k steps. Image taken from [4]
To implement this idea, we need to train a model predicting the steps between two observations. To simplify, we can predefine the threshold k, and create a model to classify whether two observations are separated by more or less than k steps.The model, named reachability network, takes 2 observations as input and outputs a logit score, performing binary classification and is trained on data collected from the agent interacting with the environment. After training, the reachability network is used to estimate the novelty of the current observation in the episode given the episodic memory M, which finally is used to compute the intrinsic reward. The training and inference procedures are depicted below:
Training and inference using the reachability network. The network predicts whether 2 observations are reachable by producing a score c (closer to 0 means not reachable and closer to 1 means reachable). Using a function F to aggregate the reachability scores between the current observation and those in the memory leads to the intrinsic reward. F can be max or 90-th percentile. Images taken from [4].
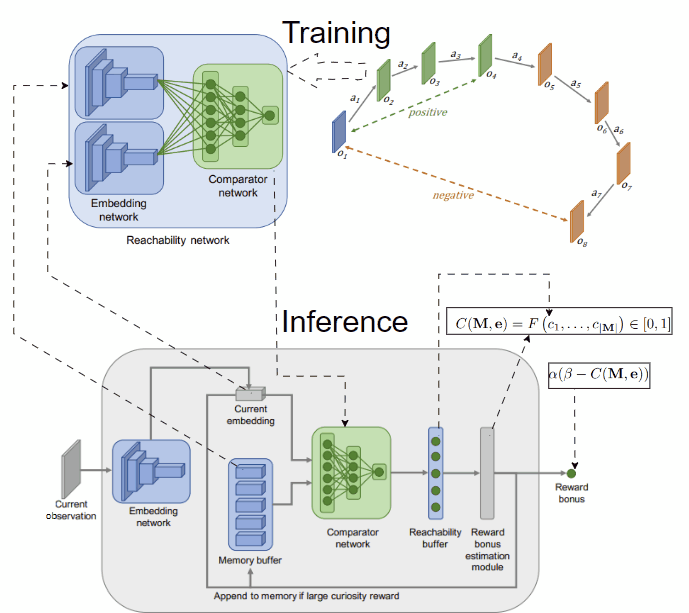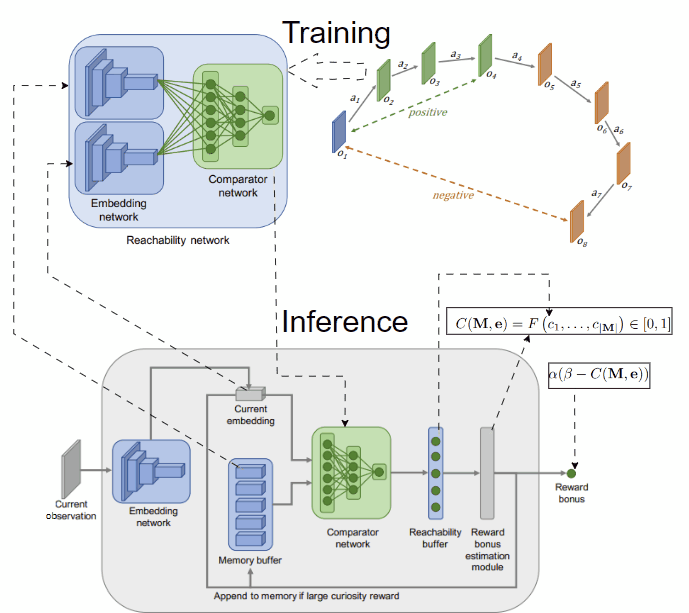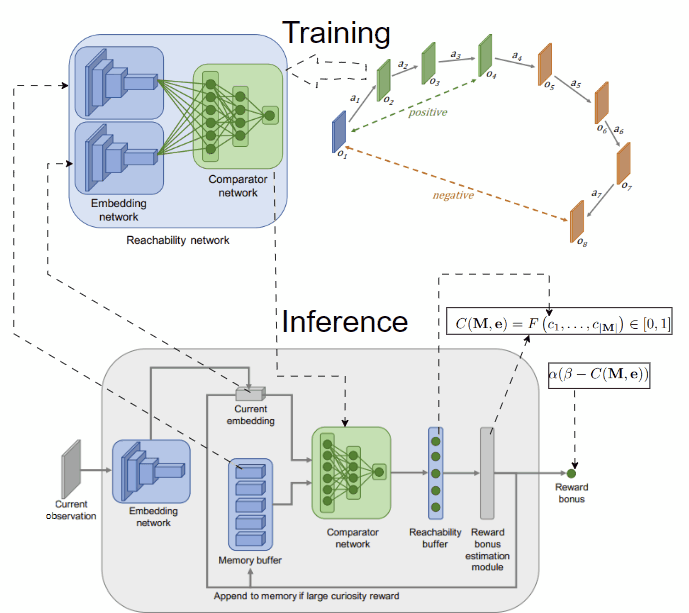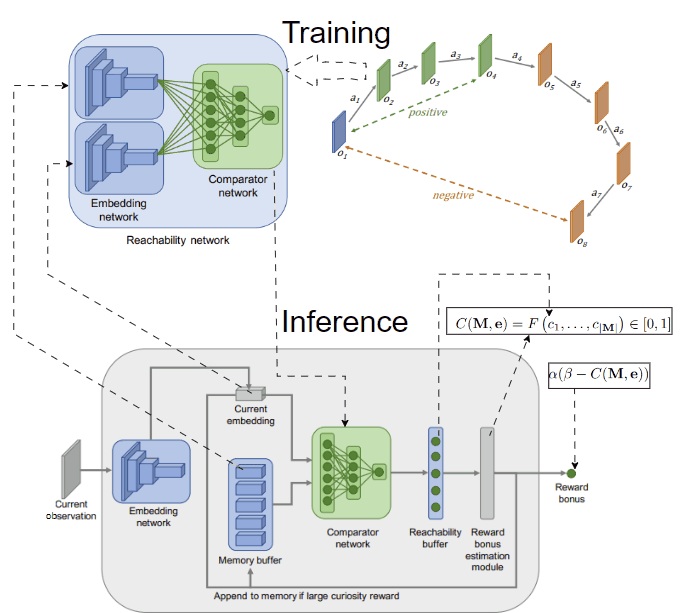
Novelty via Reconstruction
Memory plays a crucial role in identifying novel events amidst routine occurrences, and various modeling approaches can be employed to capture this functionality. As discussed earlier, memory can take the form of a straightforward counter or a buffer that retains a list of observations—characterized as non-parametric memory. In this section, our interest lies in exploring parametric memory models, particularly those embodied by autoencoder neural network architectures.
Theoretically, an overparameterized autoencoder whose task is to reconstruct its input is equivalent to an associative memory [14]. Therefore, we can train an autoencoder that takes the state as input to reconstruct and use its reconstruction error as an indicator of novelty, i.e., 👉autoencoder novelty [15]. Greater errors signify a higher level of novelty in states, indicating that the autoencoder has not encountered these states frequently enough to learn their successful reconstruction effectively.
It turns out that even for random targets, reconstruction can still contribute to the exploration process. In 👉Random Network Distillation (RND, [16]), the intrinsic reward is defined through the task of predicting the output of a fixed (target) network whose weights are random, as shown in the figure below:
RND: given the state as inputs, one neural network (green) is trained to predict the other network (blue) output. The prediction error is the intrinsic reward.
The intrinsic reward is still the reconstruction error. But this time, the reconstructed target is no longer the original input. Instead, it is a transformed version of the input.
👀 As you can see, through various means, novelty can be modeled and implemented in RL exploration. However, this is not the only source of motivation for agent curiosity. We will see more in the upcoming sections.
Surprise
Psychologically, surprise emerges when there's a discrepancy between expectations and the observed or experienced reality [5]. We, as humans, rely heavily on surprise to navigate our actions through life. Think back to the last time you encountered something unexpected, like an unpleasant odor or a road accident; the instinct is to immediately investigate what is happening. Inspired by this behavior, researchers have made numerous attempts to model surprise in RL agents, aiming to enhance their exploration of the environment. 🧠 What is the mechanism for comparing an expectation with actuality to model surprise?
Predictive Surprise
One approach is to build a model of the environment, predicting the next state given the current state and action. This kind of model, also known as 👉forward dynamics or world model [6], provides a mechanism for estimating the expectation of the agent observation. In [7], the authors propose to use a neural network f that takes a representation of the current state and action to predict the next state.
👀 A nuanced yet pivotal distinction between dynamics prediction and state reconstruction (in autoencoder novelty) is the involvement of next state prediction in the former. Predicting the future is inherently more challenging than reconstructing the current observations.
The representation is shaped through unsupervised training, i.e., state reconstruction task, using an autoencoder’s hidden state. The network f, fed with the autoencoder’s hidden state, is trained to minimize the prediction error, which is the norm of the difference between the predicted state and the true state.
Surprise as dynamics model prediction error. Image taken from [7]
Here, the intrinsic reward is synonymous with the prediction error itself. This reward increases when the model encounters difficulty in predicting or expresses surprise at the current observation.
Apart from using an autoencoder, one may use different methods to learn a good representation because predicting raw observation is very hard. 👉Intrinsic Curiosity Module (ICM) [8] advocates for a state feature space that excludes uncontrollable factors that do not influence the agent's behavior, providing no incentive for learning. To learn state embeddings that enable controllable space, ICM employs an inverse dynamic model g predicting the action given 2 consecutive state representations 𝜙.
To make predictions accurately, the representations must be meaningful and action-oriented. Combined with forward dynamics prediction, ICM proposes the intrinsic reward as
An alternative method with forward dynamics involves using the variance of the prediction rather than the error [10]. This requires multiple prediction models trained to minimize the forward dynamics prediction errors, and we use the empirical variance (👉disagreement) of their predictions as the intrinsic reward.
Disagreement-based intrinsic reward. Multiple dynamics models make predictions and the variance of these predictions is the intrinsic reward. Image taken from [10].
❌ Sometimes, focusing on the forward dynamics error is not effective in driving the exploration, especially when the world model is not good and always predicts wrongly.
❌ Moreover, predictive surprise becomes irrelevant in scenarios with environmental noise. Take the hypothetical case of Noisy-TV [4], where an agent can open a TV channel displaying random contents. The agent, unable to predict the randomness, consistently experiences high prediction error or surprise. Yet, engaging with the noisy TV proves useless, diverting the agent from its primary task. Example of Noisy-TV is illustrated below:
Noisy-TV: a random TV will distract the RL agent from its main task due to high surprise (source).
In [9], the authors propose using 👉learning progress as intrinsic motivation, which somehow addresses this issue. The learning progress is estimated by comparing the mean error rate of the prediction model during the current moving window to the mean error rate of the previous window. The two windows are different by 𝜏 steps.
where k is the window size. Intuitively, we aim to incentivize observations and actions that enhance learning progress.
👀 Learning progress is immune against noisy-TV because the prediction error of watching noises is always high. If the agent keeps watching TV, there will be no change in the average error over time, showing no learning progress. However, correctly estimating the learning progress is complicated and it takes a long time to monitor the progress, which is not sample-efficient.
Bayesian Surprise
Surprise can be interpreted from a Bayesian statistics perspective. Inspired by classical exploration such as information gain, the agent benefits from actions that minimize uncertainty about the dynamics, formalized as maximizing the cumulative reduction in entropy [11]:
The reduction of entropy per time step, also known as mutual information I(𝚯;St+1|ξt,at), is computed explicitly as:
Here θ is the parameters of the dynamics model 𝚯. Because we are interested in finding intrinsic reward for a given timestep, we can define:
Unfortunately, the KL involves computing the posterior p(θ|st+1), which is generally intractable. Hence, the authors in [11] turn to variational inference for approximating the posterior. Specifically, then they use an alternative variational distribution q(θ; 𝜙):
where 𝜙is the variational parameter. This is equivalent to parameterizing the dynamics model as a Bayesian neural network (BNN) with weight distributions maintained as a fully factorized Gaussian. The network can be trained by the following minimization:
Finally, we can use the trained variational distribution to compute the intrinsic reward or 👉Bayesian information gain:
Training a BNN is complicated, so Achiam and Sastry (2017) propose a different Bayesian view on surprise [12]. First, they formulate the objective of the RL agent as jointly maximizing expected return and surprise:
where P is the true dynamics model and P𝜙 is the learned dynamics model. It makes sense to model the surprise as the expected divergence between the observation and the predicted. The objective can be translated to maximizing the bonus reward per step:
In practice, we do not know P. Therefore, the authors propose an approximation:
👀 This bonus term is similar to the prediction error. It just measures the error in log probability instead of the norm of the difference between the predicted and the reality.
Another proposed approximation is:
Here, the intrinsic reward is essentially the learning progress written in the form of log probability (👉Bayesian learning progress). To train the dynamics model P𝜙, the authors solve the constrained optimization:
👀 By introducing the KL constraint, the posterior model is prevented from diverging too far from the prior, thereby preventing the generation of unstable intrinsic rewards.
The Bayesian surprises studied above are defined by a specific dynamics model. 🧠 What happens if we consider a distribution of models? In [13], the authors formulate Bayesian surprise as Information Gain given a policy π as:
where P(T) is the transition distribution of the environment and P(T|𝜙) is the transition distribution according to the dynamics model. The term u(s,a), which models some form of 👉Bayesian disagreement, turns out to be the Jensen-Shannon Divergence of a set of learned dynamics from a transition dynamics t:
where P(S|s,a,t) is the dynamics model learned from a transition dynamics t. Here, we used the property that Jensen-Shannon divergence is the entropy of the average minus the average of the entropies. In practice, this JSD can be approximated by employing N dynamics models:
For each P parameterized by Gaussian distribution 𝓝i(µi,Σi), we need another layer of approximation to compute u(s,a). Particularly, the authors propose to replace the Shannon entropy with Rényi entropy and use the corresponding Jensen-Rényi Divergence (JRD):
❌ While these Bayesian views are theoretically rigorous, they face challenges with intricate computations of the posterior for dynamics models or the necessity to monitor multiple models throughout the training. They also make a lot of assumption and approximations that may go wrong in practice.
Hybrid Approaches
It didn't take long for researchers to recognize the potential marriage between surprise and novelty. The amalgamation of surprise and novelty constitutes a potent strategy to enhance the exploration capabilities of reinforcement learning agents.
Surprise + Novelty
The 👉Never Give Up agent (NGU), introduced in [17], combines existing surprise and novelty components from the literature cleverly:
State representation learning via inverse dynamics [8]
Life-long novelty module using RND [16]
Episodic novelty using episodic memory inspired by EC [4]. Note that the implementation of the memory in NGU is new.
This mix-up results in a very powerful exploration architecture, as depicted below:
Never Give Up: The dynamics model f is employed to produce the representations for the novelty modules. Two types of novelty are combined to produce the final intrinsic reward. Image taken from [17].
The most interesting component is the episodic novelty, which encourages the exploration of novel states within an episode simply via nearest-neighbor matching. As a result, the agent will not revisit the same state in an episode twice. This concept is different from lifelong novelty as explained by the author:
The episodic intrinsic reward promotes the agent to visit as many different states as possible within a single episode. This means that the notion of novelty ignores inter-episode interactions: a state that has been visited thousands of times gives the same intrinsic reward as a completely new state as long as they are equally novel given the history of the current episode.
A life-long (or inter-episodic) novelty module provides a long-term novelty signal to statefully control the amount of exploration across episodes
—Text taken from [17]—
The authors implement the episodic intrinsic reward as:
where Nk nearest neighbor of the current state representation is retrieved from the episodic memory to compute the weighted sum of similarity to form the reward. The closer the current state is to its neighbors, the higher the similarity and thus, the smaller the reward. K is a function measuring the similarity and c is a hyperparameter guarding from divide-by-zero issues.
The ultimate intrinsic reward is:
where L is a hyperparameter and σe and µe are running standard deviation and mean for RND(x), contributing to normalizing the RND’s rewards. By utilizing both the episode and long-life novelty, the NGU agent quickly avoids revisiting the same state within a single episode and gradually stays away from states that have been encountered frequently across multiple episodes.
Later, the authors propose an upgraded version of the NGU, called 👉Agent57 [18], with several improvements:
Splitting the value function into 2 separate function values for external and internal rewards.
A population of policies (and value functions) is trained, each characterized by a distinct pair of exploration parameters:
where N is the size of the population. 𝛾j is the discount factor hyperparameters and βj is the intrinsic reward coefficient hyperparameters. These values are adaptively determined during training using a sliding-window UCB bandit algorithm (meta controller) where the policy corresponding to the hyperparameter j is trained and evaluated to compute a performance metric maximized by the meta controller.
👀 Agent 57 is the first method that can beat humans in all 57 Atari games, as reported in the following figure:
Agent 57 outperforms humans in 57 Atari games after 1e10 training frames. Image taken from [18].
This hybrid approach incorporates separate modules for surprise and novelty. 🧠 Are there alternative methods to blend the two concepts?
Novelty of Surprise
Recently, Le et al. (2024) have proposed a new approach that leverages both surprise and novelty elements in a single exploration architecture [15]. The authors start from an observation that the norm of the prediction error (surprise norm) cannot fully capture the incentive because a high surprise norm may not correspond to a meaningful event (e.g., as in Noisy-TV). They propose a new metric, namely the novelty of the surprise or 👉surprise novelty. To identify surprise novelty, the agent needs to compare the current surprise with surprises in past encounters and use the novelty of the surprise as the intrinsic reward rather than its norm.
Surprise norm vs surprise novelty in Montezuma Revenge. Interesting states have a better reflection on the surprise novelty. Images taken from [15].
Based on that principle, they operate novelty-based exploration approaches on surprise space rather than state space. This requires a surprise generator such as a dynamics model to produce the surprise vector u, i.e., the difference vector between the predicted and reality. Then, inter and intra-episode novelty scores are estimated by a system of memory, called Surprise Memory (SM), consisting of an autoencoder network W and episodic memory M, respectively.
Surprise novelty is estimated through surprise memory architecture (SM). Image taken from [15].
This design is similar to NGU with lifelong and episodic novelty modules. However, the implementation promotes some new ideas:
The episodic memory retrieval is trainable through an attention mechanism rather than using a fixed nearest neighbor retrieval, which allows flexible adaptation to specific tasks and environments.
The inter-episode novelty is estimated by an autoencoder rather than RND.
The novelty operates on surprise space rather than observation space.
The workflow of the two memory modules is summarized below:
The gist of the algorithm is the episodic surprise ue is concatenated with the surprise u of observation, and the autoencoder W tries to reconstruct the concatenation to estimate its novelty.
👀 The technique is very effective under a low-sample regime where Atari games are trained for only 50 million frames.
🧠 Beyond novelty and surprise, what other strategies can enhance exploration in Reinforcement Learning? Discover the answer in the third part of my post series.
[1] Bellemare, Marc, Sriram Srinivasan, Georg Ostrovski, Tom Schaul, David Saxton, and Remi Munos. "Unifying count-based exploration and intrinsic motivation." Advances in neural information processing systems 29 (2016).
[2] Tang, Haoran, Rein Houthooft, Davis Foote, Adam Stooke, OpenAI Xi Chen, Yan Duan, John Schulman, Filip DeTurck, and Pieter Abbeel. "# exploration: A study of count-based exploration for deep reinforcement learning." Advances in neural information processing systems 30 (2017).
[3] Parisi, Simone, Victoria Dean, Deepak Pathak, and Abhinav Gupta. "Interesting object, curious agent: Learning task-agnostic exploration." Advances in Neural Information Processing Systems 34 (2021): 20516-20530.
[4] Savinov, Nikolay, Anton Raichuk, Raphaël Marinier, Damien Vincent, Marc Pollefeys, Timothy Lillicrap, and Sylvain Gelly. "Episodic curiosity through reachability." arXiv preprint arXiv:1810.02274 (2018).
[5] Ekman, P., and Davidson, R. J. (eds.). (1994). The Nature of Emotion: Fundamental Questions. Oxford: Oxford University Press.
[6] Schmidhuber, Jürgen. "A possibility for implementing curiosity and boredom in model-building neural controllers." In Proc. of the international conference on simulation of adaptive behavior: From animals to animats, pp. 222-227. 1991.
[7] Stadie, Levine, Abbeel: Incentivizing Exploration in Reinforcement Learning with Deep Predictive Models. In NIPS 2015.
[8] Pathak, Deepak, Pulkit Agrawal, Alexei A. Efros, and Trevor Darrell. "Curiosity-driven exploration by self-supervised prediction." In International conference on machine learning, pp. 2778-2787. PMLR, 2017.
[9] Pierre-Yves Oudeyer & Frederic Kaplan. “How can we define intrinsic motivation?” Conf. on Epigenetic Robotics, 2008.
[10] Deepak Pathak, et al. “Self-Supervised Exploration via Disagreement.” In ICML 2019.
[11] Houthooft, Rein, Xi Chen, Yan Duan, John Schulman, Filip De Turck, and Pieter Abbeel. "Vime: Variational information maximizing exploration." Advances in neural information processing systems 29 (2016).
[12] Joshua Achiam and Shankar Sastry. 2017. Surprise-based intrinsic motivation for deep reinforcement learning. arXiv preprint arXiv:1703.01732 (2017).
[13] Pranav Shyam, Wojciech Jaskowski, and Faustino Gomez. 2019. Model-Based Active Exploration. In Proceedings of the 36th International Conference on Machine Learning, ICML 2019, 9-15 June 2019, Long Beach, California, USA. 5779–5788.
[14] Adityanarayanan Radhakrishnan, Mikhail Belkin, and Caroline Uhler. 2020. Overparameterized neural networks implement associative memory. Proceedings of the National Academy of Sciences 117, 44 (2020), 27162–27170.
[15] Le, Hung, Kien Do, Dung Nguyen, and Svetha Venkatesh. "Beyond Surprise: Improving Exploration Through Surprise Novelty. In AAMAS, 2024.
[16] Burda, Yuri, Harrison Edwards, Amos Storkey, and Oleg Klimov. "Exploration by random network distillation." In International Conference on Learning Representations. 2018.
[17] Badia, Adrià Puigdomènech, Pablo Sprechmann, Alex Vitvitskyi, Daniel Guo, Bilal Piot, Steven Kapturowski, Olivier Tieleman et al. "Never give up: Learning directed exploration strategies." arXiv preprint arXiv:2002.06038 (2020).
[18] Badia, Adrià Puigdomènech, Bilal Piot, Steven Kapturowski, Pablo Sprechmann, Alex Vitvitskyi, Zhaohan Daniel Guo, and Charles Blundell. "Agent57: Outperforming the atari human benchmark." In International conference on machine learning, pp. 507-517. PMLR, 2020.
I hope you enjoy the article. Stay tuned for the newest and exclusive content by subscribing to Neurocoder Tales! Disclaimer:While every effort is made to provide accurate and unbiased information, errors may occur. Let me know if you catch any error.
